题目内容
已知M=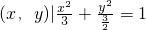
，N=（x，y）|y=mx+b，若对于所有的m∈R，均有M∩N≠φ，则b的取值范围是
- A.
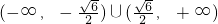
- B.（
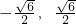） - C.[]
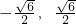- D.[
]
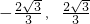C
分析：由题意可得直线y=mx+b 上的点（0，b） 在椭圆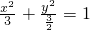
的内部或在椭圆上，故有 0+
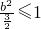，解不等式
求得b的取值范围．
解答：由题意可得直线y=mx+b 上的点（0，b） 在椭圆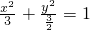 的内部或在椭圆上，
故有 0+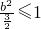，解得 b2≤
，-
≤b≤，
故选C．
点评：本题考查两个集合的交集的定义，直线和椭圆相交的条件，判断点点（0，b） 在椭圆的内部或在椭圆上，是解题的关键．
分析：由题意可得直线y=mx+b 上的点（0，b） 在椭圆
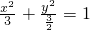的内部或在椭圆上，故有 0+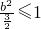，解不等式求得b的取值范围．
解答：由题意可得直线y=mx+b 上的点（0，b） 在椭圆
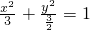的内部或在椭圆上，故有 0+
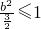，解得 b2≤，-≤b≤，故选C．
点评：本题考查两个集合的交集的定义，直线和椭圆相交的条件，判断点点（0，b） 在椭圆的内部或在椭圆上，是解题的关键．
练习册系列答案
相关题目
已知m，n是关于x的一元二次方程x2-3x+a=0的两个解，若（m-1）（n-1）=-6，则a的值为（ ）
| A、-10 | B、4 | C、-4 | D、10 |
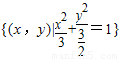，N=（x，y）|y=mx+b，若对于所有的m∈R，均有M∩N≠φ，则b的取值范围是（ ）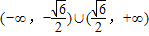
）
]
]
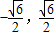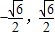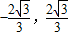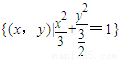，N=（x，y）|y=mx+b，若对于所有的m∈R，均有M∩N≠φ，则b的取值范围是（ ）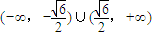
）
]
]
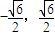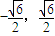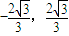