题目内容
设x、y∈R,集合A={(x,y)|x2-y2=1},B={(x,y)|y=t(x+2)+3},若A∩B为单元素集,则t值的个数是( )A.1
B.2
C.3
D.4
【答案】分析:先弄清两集合所表示的几何意义,然后结合图象可知直线与双曲线相切的直线有两条,与渐近线平行的直线有两条,这四条直线都与双曲线只有一个交点,从而A∩B为单元素集,即可求出所求.
解答:解:集合A表示等轴双曲线上的点的集合;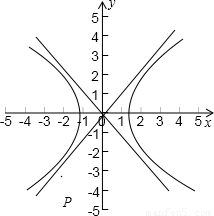
集合B表示恒过点(-2,3)的点的集合;
结合图象,直线与双曲线相切的直线有两条,
与渐近线平行的直线有两条,这四条直线都与双曲线只有一个交点
从而A∩B为单元素集
∴t值的个数是4
故选D.
点评:本题主要考查了直线与圆锥曲线的交点个数问题,同时考查了转化的数学思想,属于中档题.
解答:解:集合A表示等轴双曲线上的点的集合;

集合B表示恒过点(-2,3)的点的集合;
结合图象,直线与双曲线相切的直线有两条,
与渐近线平行的直线有两条,这四条直线都与双曲线只有一个交点
从而A∩B为单元素集
∴t值的个数是4
故选D.
点评:本题主要考查了直线与圆锥曲线的交点个数问题,同时考查了转化的数学思想,属于中档题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目