题目内容
已知正项数列![]() 满足:对任意正整数
满足:对任意正整数![]() ,都有
,都有![]() 成等差数列,
成等差数列,![]() 成等比数列,且
成等比数列,且![]()
(Ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ) 设![]() 如果对任意正整数
如果对任意正整数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(1)由已知,得![]() ①,
①,![]() ② . 由②得
② . 由②得![]() ③.
③.
将③代入①得,对任意![]() ,有
,有![]()
即![]()
![]() 是等差数列. 4分
是等差数列. 4分
(Ⅱ)设数列![]() 的公差为
的公差为![]() ,
,
由![]() 经计算,得
经计算,得![]()
![]()
![]()
![]()
![]() 9分
9分
(Ⅲ)由(1)得![]()
![]()
不等式![]() 化为
化为![]()
即![]()
设![]()
![]() ,则
,则![]() 对任意正整数
对任意正整数![]() 恒成立.
恒成立.
当![]() ,即
,即![]() 时,不满足条件;
时,不满足条件;
当![]() ,即
,即![]() 时,满足条件;
时,满足条件;
当![]() ,即
,即![]() 时,
时,![]() 的对称轴为
的对称轴为![]() ,
,![]() 关于
关于![]() 递减,
递减,
因此,只需![]() 解得
解得![]()
综上,![]() 14分
14分

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
(本题满分14分)
已知正项数列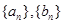 满足:对任意正整数
满足:对任意正整数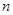 ,都有
,都有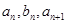 成等差数列,
成等差数列,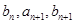 成等比数列,且
成等比数列,且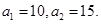
(Ⅰ)求证:数列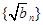 是等差数列;
是等差数列;
(Ⅱ)求数列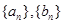 的通项公式;
的通项公式;
(Ⅲ) 设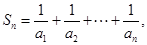 如果对任意正整数
如果对任意正整数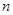 ,不等式
,不等式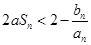 恒成立,求实数
恒成立,求实数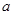 的取值范围.
的取值范围.
 满足:对任意正整数
满足:对任意正整数 ,都有
,都有 成等差数列,
成等差数列, 成等比数列,且
成等比数列,且
 是等差数列;
是等差数列;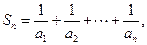 如果对任意正整数
如果对任意正整数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.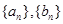 满足:对任意正整数
满足:对任意正整数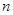 ,都有
,都有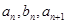 成等差数列,
成等差数列,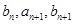 成等比数列,且
成等比数列,且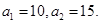
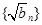 是等差数列;
是等差数列;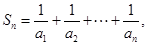 如果对任意正整数
如果对任意正整数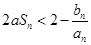 恒成立,求实数
恒成立,求实数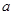 的取值范围.
的取值范围.