题目内容
 =(1,1),
=(1,1), =(1,0),
=(1,0), 满足
满足 =0,且
=0,且 =
=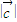 ,
,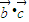 >0
>0(I)求向量
 ;
;(II)若映射

①求映射f下(1,2)原象;
②若将(x、y)作点的坐标,问是否存在直线l使得直线l上任一点在映射f的作用下,仍在直线上,若存在求出l的方程,若不存在说明理由.
【答案】分析:(I)设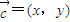 ,由已知得到关于x、y的方程组,求出x、y,即求得向量
,由已知得到关于x、y的方程组,求出x、y,即求得向量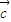 ;
;
(II)根据映射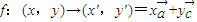 ,①求映射f下(1,2)原象,列出方程,解方程即可;②存在性命题的探讨,转化为(1+k)y=(1-k)x-b与y=kx+b表示同一直线,对应系数相等,求得直线方程.
,①求映射f下(1,2)原象,列出方程,解方程即可;②存在性命题的探讨,转化为(1+k)y=(1-k)x-b与y=kx+b表示同一直线,对应系数相等,求得直线方程.
解答:解:(I)设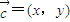 ,则
,则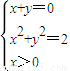
∴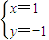
∴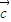 =(1,-1)
=(1,-1)
(II)①x(1,1)+y(1,-1)=(1,2)
∴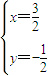
∴原象是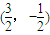
②假设l存在,设其方程为y=kx+b(k≠0),
∴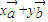 =(x+y,x-y)
=(x+y,x-y)
点(x+y,x-y)在直线上
∴x-y=k(x+y)+b
即(1+k)y=(1-k)x-b与y=kx+b表示同一直线,
必有-b=b,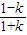 =k,
=k,
解可得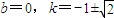 ,
,
∴直线?存在其方程为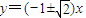 .
.
点评:考查平面向量的坐标运算和数量积,属基础题,对映射的定义,增加了试题新颖和综合,体现了转化和方程的思想方法,很好.
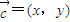 ,由已知得到关于x、y的方程组,求出x、y,即求得向量
,由已知得到关于x、y的方程组,求出x、y,即求得向量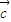 ;
;(II)根据映射
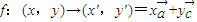 ,①求映射f下(1,2)原象,列出方程,解方程即可;②存在性命题的探讨,转化为(1+k)y=(1-k)x-b与y=kx+b表示同一直线,对应系数相等,求得直线方程.
,①求映射f下(1,2)原象,列出方程,解方程即可;②存在性命题的探讨,转化为(1+k)y=(1-k)x-b与y=kx+b表示同一直线,对应系数相等,求得直线方程.解答:解:(I)设
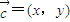 ,则
,则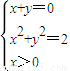
∴
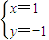
∴
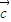 =(1,-1)
=(1,-1)(II)①x(1,1)+y(1,-1)=(1,2)
∴
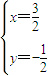
∴原象是
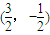
②假设l存在,设其方程为y=kx+b(k≠0),
∴
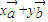 =(x+y,x-y)
=(x+y,x-y)点(x+y,x-y)在直线上
∴x-y=k(x+y)+b
即(1+k)y=(1-k)x-b与y=kx+b表示同一直线,
必有-b=b,
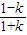 =k,
=k,解可得
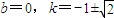 ,
,∴直线?存在其方程为
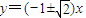 .
.点评:考查平面向量的坐标运算和数量积,属基础题,对映射的定义,增加了试题新颖和综合,体现了转化和方程的思想方法,很好.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
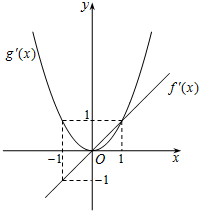 (2013•武汉模拟)已知函数f'(x)、g'(x)分别是二次函数f(x)和三次函数g(x)的导函数,它们在同一坐标系下的图象如图所示:
(2013•武汉模拟)已知函数f'(x)、g'(x)分别是二次函数f(x)和三次函数g(x)的导函数,它们在同一坐标系下的图象如图所示: ,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个. ,an+1=f(an),bn=
,an+1=f(an),bn= -1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
-1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式; .…………………………………………4分
.…………………………………………4分 (n∈N*),bn=
(n∈N*),bn= =
= =
= =
= ,
, -1=
-1= n-1=
n-1= =1-an=1-
=1-an=1- =
= ,
,  +
+ +…+
+…+ +
+ +…+
+…+
 =1-
=1-