题目内容
有一数列{an},a1=a,由递推公式an+1=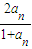 ,写出这个数列的前4项,并根据前4项观察规律,写出该数列的一个通项公式.
,写出这个数列的前4项,并根据前4项观察规律,写出该数列的一个通项公式.
【答案】分析:可根据递推公式写出数列的前4项,然后分析每一项与该项的序号之间的关系,归纳概括出an与n之间的一般规律,从而作出猜想,写出满足前4项的该数列的一个通项公式.
解答:解:∵a1=a,an+1=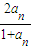 ,∴a2=
,∴a2=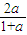 ,
,
a3=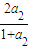 =
=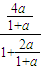 =
=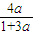 ,
,
a4=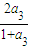 =
=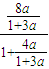 =
=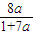 .
.
观察规律:an=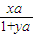 形式,其中x与n的关系可由n=1,2,3,4得出x=2n-1.而y比x小1,
形式,其中x与n的关系可由n=1,2,3,4得出x=2n-1.而y比x小1,
∴an=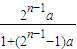 .
.
点评:从特殊的事例,通过分析、归纳、抽象总结出一般规律,再进行科学地证明,这是创新意识的具体体现,这种探索问题的方法,在解数列的有关问题中经常用到,应引起足够的重视.
解答:解:∵a1=a,an+1=
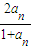 ,∴a2=
,∴a2=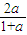 ,
,a3=
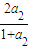 =
=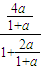 =
=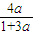 ,
,a4=
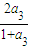 =
=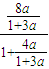 =
=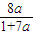 .
.观察规律:an=
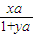 形式,其中x与n的关系可由n=1,2,3,4得出x=2n-1.而y比x小1,
形式,其中x与n的关系可由n=1,2,3,4得出x=2n-1.而y比x小1,∴an=
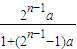 .
.点评:从特殊的事例,通过分析、归纳、抽象总结出一般规律,再进行科学地证明,这是创新意识的具体体现,这种探索问题的方法,在解数列的有关问题中经常用到,应引起足够的重视.

练习册系列答案
相关题目
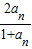 ,写出这个数列的前4项,并根据前4项观察规律,写出该数列的一个通项公式.
,写出这个数列的前4项,并根据前4项观察规律,写出该数列的一个通项公式.