题目内容
科研室的老师为了研究某班学生数学成绩x与英语成绩y的相关性,对该班全体学生的某次期末检测的数学成绩和英语成绩进行统计分析,利用相关系数公式r=
,计算得r=-0.001,并且计算得到线性回归方程为y=bx+a,其中b=
,a=
-b
.由此得该班全体学生的数学成绩x与英语成绩y相关性的下列结论正确的是( )
| ||||||||||
|
| ||||||
|
. |
| y |
. |
| x |
分析:由相关系数的性质:-1<r<1,r<0时说明变量间为负相关,r>0时说明变量间为正相关,|r|越大,相关性越强,一般认为当|r|≥0.75时,认为相关性较强.对照这些性质即可作出正确选择
解答:解:∵相关系数r=-0.001<0,∴班全体学生的数学成绩x与英语成绩y相关性为负相关
∵相关系数r=-0.001的绝对值为0.001,远远小于0.75,∴班全体学生的数学成绩x与英语成绩y相关性较弱
故选D
∵相关系数r=-0.001的绝对值为0.001,远远小于0.75,∴班全体学生的数学成绩x与英语成绩y相关性较弱
故选D
点评:本题考察了变量的相关系数的性质,线性回归方程的意义,掌握相关系数的性质是解决本题的关键

练习册系列答案
相关题目
科研室的老师为了研究某班学生数学成绩x与英语成绩y的相关性,对该班全体学生的某次期末检测的数学成绩和英语成绩进行统计分析,利用相关系数公式r=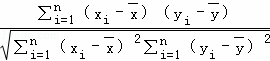 ,计算得r=﹣0.001,并且计算得到线性回归方程为y=bx+a,其中b=
,计算得r=﹣0.001,并且计算得到线性回归方程为y=bx+a,其中b=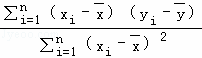 ,a=
,a=![]() .由此得该班全体学生的数学成绩x与英语成绩y相关性的下列结论正确的是( )
.由此得该班全体学生的数学成绩x与英语成绩y相关性的下列结论正确的是( )
|
| A. | 相关性较强且正相关 | B. | 相关性较弱且正相关 |
|
| C. | 相关性较强且负相关 | D. | 相关性较弱且负相关 |
 ,计算得r=-0.001,并且计算得到线性回归方程为y=bx+a,其中b=
,计算得r=-0.001,并且计算得到线性回归方程为y=bx+a,其中b= ,a=
,a= .由此得该班全体学生的数学成绩x与英语成绩y相关性的下列结论正确的是( )
.由此得该班全体学生的数学成绩x与英语成绩y相关性的下列结论正确的是( )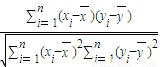 ,计算得r=-0.001,并且计算得到线性回归方程为y=bx+a,其中b=
,计算得r=-0.001,并且计算得到线性回归方程为y=bx+a,其中b=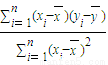 ,a=
,a= .由此得该班全体学生的数学成绩x与英语成绩y相关性的下列结论正确的是( )
.由此得该班全体学生的数学成绩x与英语成绩y相关性的下列结论正确的是( )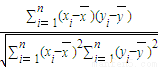 ,计算得r=-0.001,并且计算得到线性回归方程为y=bx+a,其中b=
,计算得r=-0.001,并且计算得到线性回归方程为y=bx+a,其中b=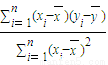 ,a=
,a= .由此得该班全体学生的数学成绩x与英语成绩y相关性的下列结论正确的是( )
.由此得该班全体学生的数学成绩x与英语成绩y相关性的下列结论正确的是( )