题目内容
已知双曲线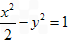 的两焦点为
的两焦点为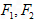 ,P为动点,若
,P为动点,若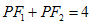 ,
,
(Ⅰ)求动点P的轨迹E方程;
(Ⅱ)若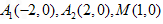 ,设直线l过点M,且与轨迹E交于R、Q两点,直线
,设直线l过点M,且与轨迹E交于R、Q两点,直线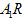 与
与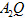 交于点S,试问:当直线l在变化时,点S是否恒在一条定直线上?若是,请写出这条定直线方程,并证明你的结论;若不是,请说明理由.
交于点S,试问:当直线l在变化时,点S是否恒在一条定直线上?若是,请写出这条定直线方程,并证明你的结论;若不是,请说明理由.
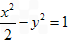 的两焦点为
的两焦点为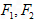 ,P为动点,若
,P为动点,若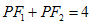 ,
,(Ⅰ)求动点P的轨迹E方程;
(Ⅱ)若
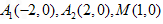 ,设直线l过点M,且与轨迹E交于R、Q两点,直线
,设直线l过点M,且与轨迹E交于R、Q两点,直线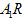 与
与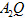 交于点S,试问:当直线l在变化时,点S是否恒在一条定直线上?若是,请写出这条定直线方程,并证明你的结论;若不是,请说明理由.
交于点S,试问:当直线l在变化时,点S是否恒在一条定直线上?若是,请写出这条定直线方程,并证明你的结论;若不是,请说明理由.解:(Ⅰ)由题意知: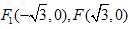 ,又∵
,又∵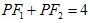 ,
,
∴动点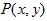 必在以
必在以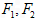 为焦点,长轴长为4的椭圆,
为焦点,长轴长为4的椭圆,
∴a=2,
又∵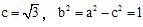 ,
,
∴椭圆C的方程为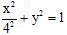 .
.
(Ⅱ)由题意,可设直线l为: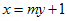
取m=0,得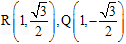 ,直线
,直线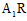 的方程是
的方程是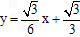
直线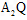 的方程是
的方程是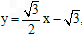 ,交点为
,交点为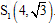 ,
,
若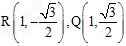 ,由对称性可知交点为
,由对称性可知交点为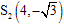 ,若点S在同一条直线上,
,若点S在同一条直线上,
则直线只能为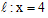
②以下证明对于任意的m,直线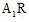 与直线
与直线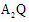 的交点S均在直线
的交点S均在直线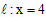 上.
上.
事实上,由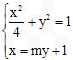 ,得
,得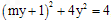 ,即
,即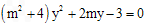 ,记
,记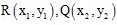 ,
,
则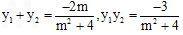 .
.
设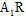 与
与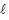 交于点
交于点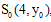 由
由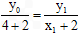 ,得
,得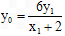 ,
,
设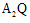 与
与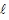 交于点
交于点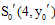 ,由
,由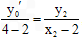 ,得
,得 ,
,
∵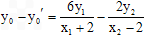 =
=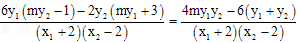 =
=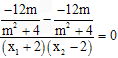 ,
,
∴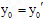 ,即
,即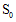 与
与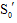 重合,
重合,
这说明,当m变化时,点S恒在定直线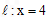 上。
上。
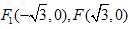 ,又∵
,又∵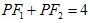 ,
,∴动点
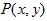 必在以
必在以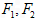 为焦点,长轴长为4的椭圆,
为焦点,长轴长为4的椭圆,∴a=2,
又∵
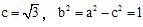 ,
,∴椭圆C的方程为
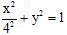 .
.(Ⅱ)由题意,可设直线l为:
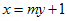
取m=0,得
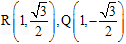 ,直线
,直线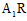 的方程是
的方程是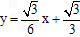
直线
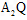 的方程是
的方程是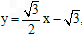 ,交点为
,交点为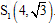 ,
,若
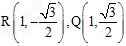 ,由对称性可知交点为
,由对称性可知交点为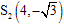 ,若点S在同一条直线上,
,若点S在同一条直线上,则直线只能为
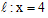
②以下证明对于任意的m,直线
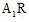 与直线
与直线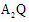 的交点S均在直线
的交点S均在直线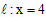 上.
上.事实上,由
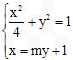 ,得
,得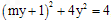 ,即
,即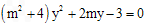 ,记
,记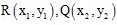 ,
,则
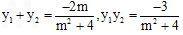 .
.设
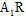 与
与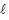 交于点
交于点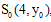 由
由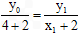 ,得
,得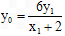 ,
,设
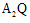 与
与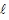 交于点
交于点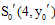 ,由
,由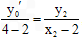 ,得
,得 ,
,∵
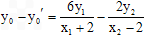 =
=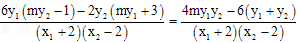 =
=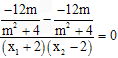 ,
,∴
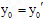 ,即
,即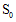 与
与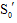 重合,
重合,这说明,当m变化时,点S恒在定直线
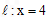 上。
上。
练习册系列答案
相关题目
 的两焦点为F、F',若该双曲线与抛物线y2=8x有一个公共的焦点F,且两曲线的一个
的两焦点为F、F',若该双曲线与抛物线y2=8x有一个公共的焦点F,且两曲线的一个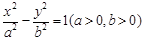 的两焦点为
的两焦点为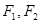 ,过
,过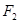 作
作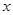 轴的垂线交双曲线于
轴的垂线交双曲线于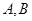 两点,若
两点,若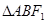 内切圆的半径为
内切圆的半径为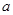 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )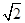 B.
B.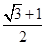 C.
C.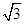 D.
D.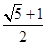
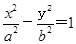 的两焦点为F1、F2,点P在双曲线上,∠F1PF2的平分线分线段F1F2的比为5 :1,则双曲线离心率的取值范围是
的两焦点为F1、F2,点P在双曲线上,∠F1PF2的平分线分线段F1F2的比为5 :1,则双曲线离心率的取值范围是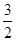 ]
B.(1,
]
B.(1,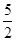 ] D.(
] D.(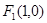 ,
,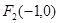 ,直线
,直线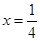 是双曲线的一条准线,
是双曲线的一条准线,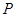 在双曲线右支上,且
在双曲线右支上,且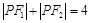 ,求
,求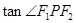 的值。
的值。