题目内容
7. 如图:点E、F、G、H分别是空间四边形的边AB、BC、CD、DA上的点,且直线EH与直线FG交于点O,求证:B、D、O三点共线.
如图:点E、F、G、H分别是空间四边形的边AB、BC、CD、DA上的点,且直线EH与直线FG交于点O,求证:B、D、O三点共线.
分析 平面ABD∩平面BDC=BD,由已知推导出O是平面ABD和平面BDC的公共点,由此能证明B、D、O三点共线.
解答 证明:∵平面ABD∩平面BDC=BD,
点E、F、G、H分别是空间四边形的边AB、BC、CD、DA上的点,且直线EH与直线FG交于点O,
∴O∈EH,O∈FG,
∵EH?平面ABD,∴O∈平面ABD,
又FG?平面BDC,∴O∈平面BDC,
∴O∈BD,
∴B、D、O三点共线.
点评 本题考查三点共线的证明,是基础题,解题时要认真审题,注意平面的基本性质及推论的证明.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
12.已知函数y=sin(ωx+θ)(0<θ<π,ω>0)为偶函数,则θ=( )
| A. | 2kπ+$\frac{π}{2}$(k∈Z) | B. | kπ+$\frac{π}{2}$(k∈Z) | C. | $\frac{π}{2}$ | D. | π |
19.椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的两个焦点为F1,F2,过F1作垂直于x轴的直线与椭圆相交,其中一个交点为P,则|PF2|的值为( )
| A. | $\frac{47}{5}$ | B. | $\frac{34}{5}$ | C. | $\frac{18}{5}$ | D. | $\frac{16}{5}$ |
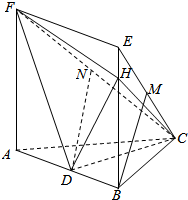 如图,在四棱锥C-ABEF中,底面ABEF是矩形,FA⊥平面ABC,点D,M,N分别是棱AB,CE.CF的中点,点H在棱BE上,且AC=BC=$\sqrt{2}$,AB=2,AF=3,BH=2.
如图,在四棱锥C-ABEF中,底面ABEF是矩形,FA⊥平面ABC,点D,M,N分别是棱AB,CE.CF的中点,点H在棱BE上,且AC=BC=$\sqrt{2}$,AB=2,AF=3,BH=2.