题目内容
设函数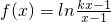 .
.
(I)当k=-1时,判断f(x)的奇偶性并给予证明;
(II)若f(x)在[e,+∞)上单调递增,求k的取值范围.
解:(Ⅰ)当k=-1时,函数 ,
,
定义域为(-1,1),关于原点对称. …
且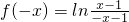 .
.
所以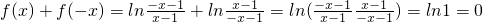 ,
,
即f(-x)=-f(x).
所以当k=-1时,函数f(x)的奇函数. …
(Ⅱ)因为y=lnu是增函数,
所以由题意, 在[e,+∞)上是增函数,且g(x)>0在[e,+∞)上恒成立. …
在[e,+∞)上是增函数,且g(x)>0在[e,+∞)上恒成立. …
即 对于x∈[e,+∞)恒成立且g(e)>0…
对于x∈[e,+∞)恒成立且g(e)>0…
所以 ,解得
,解得 .
.
所以k的取值范围是 . …
. …
分析:(I)由k=-1代入,确定函数的解析式与定义域,判断定义域是否关于原点对称,若对称再判断f(-x)与f(x)的关系,根据函数奇偶性的定义可得答案.
(II)根据复合函数的单调性,可得若f(x)在[e,+∞)上单调递增,则 在[e,+∞)上是增函数,且g(x)>0在[e,+∞)上恒成立,求导后构造关于k的不等式组,解得可得答案.
在[e,+∞)上是增函数,且g(x)>0在[e,+∞)上恒成立,求导后构造关于k的不等式组,解得可得答案.
点评:本题考查的知识点是函数奇偶性与单调性的综合应用,(I)的关键是掌握证明函数奇偶性的方法及步骤,(II)的关键是分析出 在[e,+∞)上是增函数,且g(x)>0在[e,+∞)上恒成立.
在[e,+∞)上是增函数,且g(x)>0在[e,+∞)上恒成立.
 ,
,定义域为(-1,1),关于原点对称. …
且
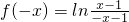 .
.所以
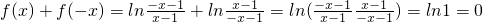 ,
,即f(-x)=-f(x).
所以当k=-1时,函数f(x)的奇函数. …
(Ⅱ)因为y=lnu是增函数,
所以由题意,
 在[e,+∞)上是增函数,且g(x)>0在[e,+∞)上恒成立. …
在[e,+∞)上是增函数,且g(x)>0在[e,+∞)上恒成立. …即
 对于x∈[e,+∞)恒成立且g(e)>0…
对于x∈[e,+∞)恒成立且g(e)>0…所以
 ,解得
,解得 .
.所以k的取值范围是
 . …
. …分析:(I)由k=-1代入,确定函数的解析式与定义域,判断定义域是否关于原点对称,若对称再判断f(-x)与f(x)的关系,根据函数奇偶性的定义可得答案.
(II)根据复合函数的单调性,可得若f(x)在[e,+∞)上单调递增,则
 在[e,+∞)上是增函数,且g(x)>0在[e,+∞)上恒成立,求导后构造关于k的不等式组,解得可得答案.
在[e,+∞)上是增函数,且g(x)>0在[e,+∞)上恒成立,求导后构造关于k的不等式组,解得可得答案.点评:本题考查的知识点是函数奇偶性与单调性的综合应用,(I)的关键是掌握证明函数奇偶性的方法及步骤,(II)的关键是分析出
 在[e,+∞)上是增函数,且g(x)>0在[e,+∞)上恒成立.
在[e,+∞)上是增函数,且g(x)>0在[e,+∞)上恒成立. 
练习册系列答案
相关题目
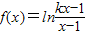 .
.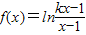 .
.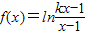 .
. .
.