题目内容
设函数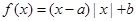
(1)当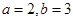 ,画出函数
,画出函数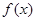 的图像,并求出函数
的图像,并求出函数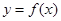 的零点;
的零点;
(2)设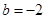 ,且对任意
,且对任意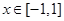 ,
,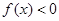 恒成立,求实数
恒成立,求实数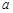 的取值范围.
的取值范围.
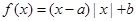
(1)当
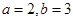 ,画出函数
,画出函数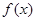 的图像,并求出函数
的图像,并求出函数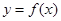 的零点;
的零点;(2)设
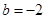 ,且对任意
,且对任意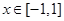 ,
,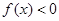 恒成立,求实数
恒成立,求实数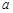 的取值范围.
的取值范围.(1)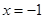 .(2)
.(2)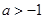 .
.
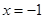 .(2)
.(2)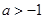 .
. 试题分析:(1)
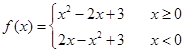 , 2分
, 2分画图正确. 4分
当
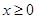 时,由
时,由 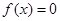 ,得
,得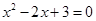 ,此时无实根;
,此时无实根;当
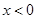 时,由
时,由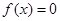 ,得
,得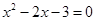 ,得
,得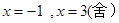 .
.所以函数的零点为
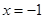 . 6分
. 6分(2)由
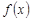 <0得,
<0得,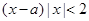 .
.当
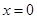 时,
时,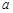 取任意实数,不等式恒成立. 8分
取任意实数,不等式恒成立. 8分当
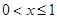 时,
时,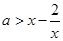 .令
.令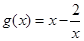 ,则
,则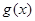 在
在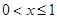 上单调递增 ,
上单调递增 ,∴
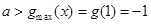 ; 10分
; 10分当
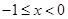 时,
时,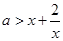 ,令
,令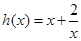 ,
, 则
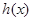 在
在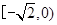 上单调递减,所以
上单调递减,所以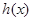 在
在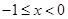 上单调递减.
上单调递减.∴
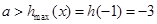 . 12分
. 12分 综合
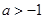 . 14分
. 14分点评:中档题,含有绝对值,因此要分类讨论,转化成分段的二次函数的图象和性质研究问题。对于不等式恒成立问题,往往转化成求函数的最值,借助于函数的单调性得解。

练习册系列答案
相关题目
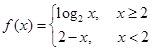 ,则满足
,则满足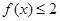 的
的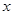 的取值范围是__________.
的取值范围是__________.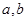 为实数,定义运算
为实数,定义运算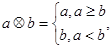 若关于
若关于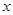 的方程
的方程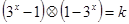 恰有两个实根,则实数
恰有两个实根,则实数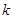 的取值范围是 ;
的取值范围是 ;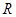 上的函数
上的函数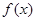 ,满足对任意
,满足对任意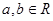 ,都有
,都有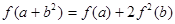 成立,则
成立,则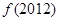 = 。
= 。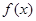 是定义在R上的奇函数,在
是定义在R上的奇函数,在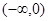 上递增,且
上递增,且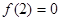 ,则使得
,则使得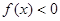 成立的
成立的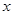 的取值范围是( )
的取值范围是( )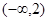



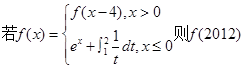 =( )
=( )
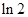
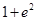
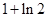
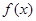 是周期为2的奇函数,当
是周期为2的奇函数,当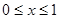 时,
时,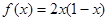 ,那么
,那么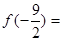
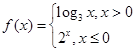 ,则
,则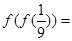
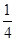 C.-4 D-
C.-4 D-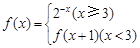 则
则 .
.