题目内容
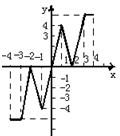 读图分析解答:设定义在闭区间[-4,4]上的函数y=f(x)的图象如图所示(图中坐标点都是实心点),完成以下几个问题:
读图分析解答:设定义在闭区间[-4,4]上的函数y=f(x)的图象如图所示(图中坐标点都是实心点),完成以下几个问题:
(1)x∈[-2,3]时,y的取值范围是________.
(2)该函数的值域为________.
(3)若y=f(x)的定义域为[-4,4],则函数y=f(x+1)的定义域为________.
(4)写出该函数的一个单调增区间为________.
(5)使f(x)=3(x∈[-4,4])的x的值有________个.
(6)函数y=f(x)是区间x∈[-4,4]的________函数.(填“奇”;“偶”或“非奇非偶”)
(7)若方程f(x)=5-3a在区间[-4,4]上有且只有三个解,求f(a)的取值范围.
 解:读图分析可得:
解:读图分析可得:(1)x∈[-2,3]时,y的取值范围是〔-4,5〕.
(2)该函数的值域为〔-5,5〕;
(3)若y=f(x)的定义域为[-4,4],则函数y=f(x+1)的定义域为〔-5,3〕.
(4)写出该函数的一个单调增区间为〔-3,-2〕或〔-1,1〕或〔2,3〕.
(5)使f(x)=3(x∈[-4,4])的x的值有3个.
(6)函数y=f(x)是区间x∈[-4,4]的奇函数.(填“奇”;“偶”或“非奇非偶”)
(7)解:如图方程f(x)=5-3a在区间[-4,4]上有且只有三个解,
则-4<5-3a<4即
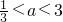 .(2分)
.(2分)又在区间[-1,1]上f(x)=4x,(4分)
 ,f(3)=5,
,f(3)=5,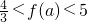 .(6分)
.(6分)故答案为:(1)〔-4,5〕,(2)〔-5,5〕,(3)〔-5,3〕,(4)〔-3,-2〕或〔-1,1〕或〔2,3〕,(5)3(6)奇,(7)
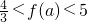 .
.分析:读图分析可得:
(1)x∈[-2,3]时,y的取值范围主要看其最大最小值即可.
(2)该函数的值域主要看y最大最小值;
(3)若y=f(x)的定义域为[-4,4],则函数y=f(x+1)的定义域为由x+1∈[-4,4],解得
(4)写出该函数的一个单调增区间主要是观察图而得.
(5)使f(x)=3(x∈[-4,4])的x的值有几个主要是看图与y=3的交点个数.
(6)观察图象的对称性可得函数y=f(x)是区间x∈[-4,4]的奇函数.
(7)解:如图方程f(x)=5-3a在区间[-4,4]上有且只有三个解,得出a的取值范围,又在区间[-1,1]上f(x)=4x,从而解决问题.
点评:本题主要考查函数的奇偶性,函数的图象等基础知识,是高考考查的重要内容,注意函数图象的灵活运用,可以使题目得到快速解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 读图分析解答:设定义在闭区间[-4,4]上的函数y=f(x)的图象如图所示(图中坐标点都是实心点),完成以下几个问题:
读图分析解答:设定义在闭区间[-4,4]上的函数y=f(x)的图象如图所示(图中坐标点都是实心点),完成以下几个问题: