题目内容
某学校举行定点投篮考试,规定每人最多投篮4次,一旦某次投篮命中,便可得到满分,不再继续以后的投篮,否则一直投到第4次为止.如果李明同学参加这次测试,设他每次定点投篮命中的概率依次为0.6,0.7,0.8,0.9.
(I)求他在本次测试中投篮次数ξ的概率分布和数学期望;
(II)求他在本次测试中得到满分的概率.
解:(I)投篮次数ξ的可能取值为1,2,3,4,则
P(ξ=1)=0.6;P(ξ=2)=0.4×0.7=0.28;P(ξ=3)=0.4×0.3×0.8=0.096;P(ξ=4)=0.4×0.3×0.2=0.024
∴ξ的概率分布列为
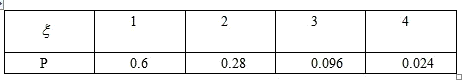
∴Eξ=1×0.6+2×0.28+3×0.096+4×0.024=1.544;
(II)记在本次测试中得到满分为事件A,则
P(A)=0.6+0.4×0.7+0.4×0.3×0.8+0.4×0.3×0.2×0.9=0.9976.
分析:(I)确定投篮次数ξ的可能取值,求出相应的概率,从而可得ξ的概率分布和数学期望;
(II)利用互斥事件的概率公式,即可求得在本次测试中得到满分的概率.
点评:本题考查离散型随机变量的概率分布和数学期望,解题的关键是确定投篮次数ξ的可能取值,求出相应的概率.
P(ξ=1)=0.6;P(ξ=2)=0.4×0.7=0.28;P(ξ=3)=0.4×0.3×0.8=0.096;P(ξ=4)=0.4×0.3×0.2=0.024
∴ξ的概率分布列为
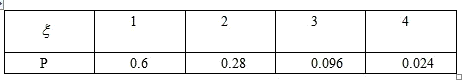
∴Eξ=1×0.6+2×0.28+3×0.096+4×0.024=1.544;
(II)记在本次测试中得到满分为事件A,则
P(A)=0.6+0.4×0.7+0.4×0.3×0.8+0.4×0.3×0.2×0.9=0.9976.
分析:(I)确定投篮次数ξ的可能取值,求出相应的概率,从而可得ξ的概率分布和数学期望;
(II)利用互斥事件的概率公式,即可求得在本次测试中得到满分的概率.
点评:本题考查离散型随机变量的概率分布和数学期望,解题的关键是确定投篮次数ξ的可能取值,求出相应的概率.

练习册系列答案
相关题目