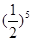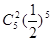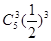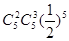题目内容
设不等式组 表示的平面区域为D.在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是 ( )
表示的平面区域为D.在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是 ( )
A. B.
B. C.
C. D.
D.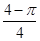
D.
解析试题分析:可行域D如图所示的边长为2的正方形,面积为S1=4,
满足到原点的距离大于2所表示的平面区域是以原点为圆心,以2为半径的圆外部,
面积为S2=4-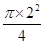 =4-π,
=4-π,
∴在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率P=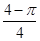
故选D.
考点:本题主要考查几何概型概率的计算。
点评:简单题,几何概型概率的计算,主要是要明确平面区域的几何度量。一般要认真分析图形特征。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
将一颗骰子抛掷两次,所得向上点数分别为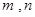 ,则函数
,则函数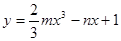 在
在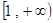 上为增函数的概率是 ( )
上为增函数的概率是 ( )
A.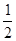 | B.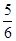 | C.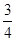 | D. |
设随机变量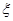 服从正态分 布
服从正态分 布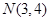 ,若
,若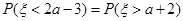 ,则
,则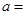 ( )
( )
A.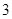 | B. | C.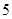 | D.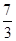 |
设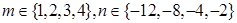 ,则函数
,则函数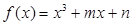 在区间
在区间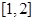 上有零点的概率是( )
上有零点的概率是( )
A.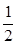 | B.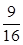 | C.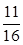 | D. |
口袋内装有大小相同的红球、白球和黑球,从中摸出一个球,摸出红球的概率是0.42,摸出白球的概率是0.28,则摸出黑球的概率是( )
| A.0.42 | B.0.28 | C.0.7 | D.0.3 |
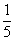
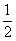
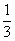
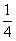
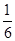
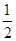



 B.
B. C.
C. D.
D.
 .质点P移动5次后位于点(2,3)的概率是( )
.质点P移动5次后位于点(2,3)的概率是( )