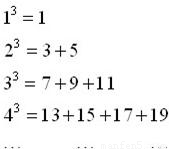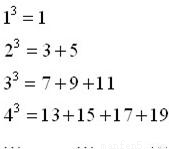题目内容
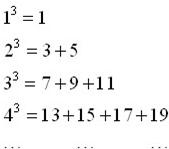 正整数m的三次幂可拆分成几个连续奇数的和,如图所示,若m3的“拆分数”中有一个数是2009,则m的值为
正整数m的三次幂可拆分成几个连续奇数的和,如图所示,若m3的“拆分数”中有一个数是2009,则m的值为
分析:先利用条件找到每一个“拆分数”中第一个数构成的数列的规律,找到其通项,再把2009代入,通过计算即可找到对应的m的值.
解答:解:设n3的“拆分数”中第一个数构成的数列为{an},
由题可知,a2-a1=2,a3-a2=4,a4-a3=6…an-an-1=2(n-1).
所以an=1+
=n2+3-3n.
当n2-3n+3=2009?n=46.31.
所以n=46不成立,故所求n=45.
故答案为:45.
由题可知,a2-a1=2,a3-a2=4,a4-a3=6…an-an-1=2(n-1).
所以an=1+
| [2+2(n-1)](n-1) |
| 2 |
当n2-3n+3=2009?n=46.31.
所以n=46不成立,故所求n=45.
故答案为:45.
点评:本题是对数列应用的考查.重点考查分析问题和解决问题以及计算方面的能力.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
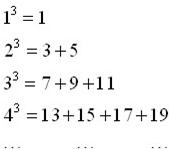 正整数m的三次幂可拆分成几个连续奇数的和,如图所示,若m3的“拆分数”中有一个数是2009,则m的值为 ________.
正整数m的三次幂可拆分成几个连续奇数的和,如图所示,若m3的“拆分数”中有一个数是2009,则m的值为 ________.