题目内容
两圆x2+y2+2ax+a2-4=0和x2+y2-4by-1+4b2=0恰有三条公切线,若a∈R,b∈R,且ab≠0,则 的最小值为
的最小值为
- A.

- B.

- C.1
- D.3
C
分析:由题意可得 两圆相外切,根据两圆的标准方程求出圆心和半径,由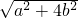 =3,得到
=3,得到 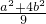 =1,
=1,
 =
=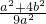 +
+ =
=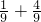 +
+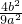 +
+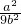 ,使用基本不等式求得
,使用基本不等式求得 的最小值.
的最小值.
解答:由题意可得 两圆相外切,两圆的标准方程分别为 (x+a)2+y2=4,x2+(y-2b)2=1,
圆心分别为(-a,0),(0,2b),半径分别为 2和1,故有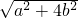 =3,∴a2+4b2=9,
=3,∴a2+4b2=9,
∴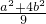 =1,∴
=1,∴ =
=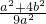 +
+ =
=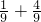 +
+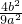 +
+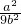
≥ +2
+2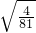 =1,当且仅当
=1,当且仅当 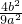 =
=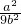 时,等号成立,
时,等号成立,
故选 C.
点评:本题考查两圆的位置关系,两圆相外切的性质,圆的标准方程的特征,基本不等式的应用,得到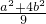 =1,
=1,
是解题的关键和难点.
分析:由题意可得 两圆相外切,根据两圆的标准方程求出圆心和半径,由
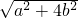 =3,得到
=3,得到 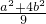 =1,
=1, =
=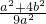 +
+ =
=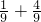 +
+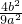 +
+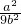 ,使用基本不等式求得
,使用基本不等式求得 的最小值.
的最小值.解答:由题意可得 两圆相外切,两圆的标准方程分别为 (x+a)2+y2=4,x2+(y-2b)2=1,
圆心分别为(-a,0),(0,2b),半径分别为 2和1,故有
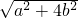 =3,∴a2+4b2=9,
=3,∴a2+4b2=9,∴
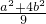 =1,∴
=1,∴ =
=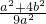 +
+ =
=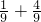 +
+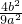 +
+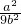
≥
 +2
+2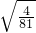 =1,当且仅当
=1,当且仅当 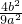 =
=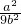 时,等号成立,
时,等号成立,故选 C.
点评:本题考查两圆的位置关系,两圆相外切的性质,圆的标准方程的特征,基本不等式的应用,得到
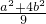 =1,
=1,是解题的关键和难点.

练习册系列答案
相关题目
过点A(a,a)可作圆x2+y2-2ax+a2+2a-3=0的两条切线,则实数a的取值范围为( )
A、a<-3或1<a<
| ||
B、1<a<
| ||
| C、a<-3 | ||
D、-3<a<1或a>
|