题目内容
在△ABC中,若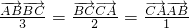 ,则tanA=________.
,则tanA=________.

分析:由题意直接列出角的正切关系,利用距离tanA+tanB+tanC=tanAtanBtanC,可得tanA的值.
解答:设△ABC中A、B、C的对应边分别为a、b、c,因为
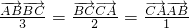 ,
,∴2accosB=3abcosC2bccosA=abcosC3bccosA=accosB
即tanA=3tanB;tanA=2tanC;
因为在△ABC中,tanA+tanB+tanC=tanAtanBtanC,
所以tanA=

故答案为:

点评:本题考查平面向量数量积的运算,正弦定理的应用,是难度较大题目.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
 ,则B的值为( )
,则B的值为( )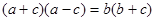 ,则∠A=( )
,则∠A=( ) B.
B. C.
C.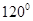 D.
D.
 ,则∠A=
,则∠A= 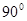 B.
B.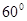 C.
C. D.
D.
 ,
, ,若
,若 ,
, ,则
,则 ()
()  A.
A. B.
B.
 D.
D.
 ,则其面积等于( )
,则其面积等于( ) B.
B. C.1
D.2
C.1
D.2