题目内容
给定椭圆![]() >b>0),称圆心在原点O,半径为
>b>0),称圆心在原点O,半径为![]() 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(![]() ,0),其短轴上的一个端点到F的距离为
,0),其短轴上的一个端点到F的距离为![]() .
.
(1)求椭圆C的方程和其“准圆”方程;
(2)点P是椭圆C的“准圆”上的一个动点,过点P作直线l1l2,使得l1l2与椭圆C都只有一个交点.求证:l1⊥l2.
答案:
解析:
解析:
|
解:(1)因为 所以椭圆的方程为 (2)①当 因为 当 此时经过点 同理可证 ②当 设经过点 则 即 经过化简得到: 因为 设 所以 所以 |

练习册系列答案
相关题目
 ,消去
,消去 >b>0),称圆心在原点O,半径为
>b>0),称圆心在原点O,半径为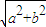 的圆是椭圆C的“伴随圆”.若椭圆C的一个焦点为
的圆是椭圆C的“伴随圆”.若椭圆C的一个焦点为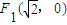 ,其短轴上的一个端点到F1的距离为
,其短轴上的一个端点到F1的距离为 .
.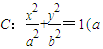 >b>0),称圆心在原点O,半径为
>b>0),称圆心在原点O,半径为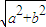 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为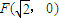 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为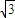 .
.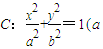 >b>0),称圆心在原点O,半径为
>b>0),称圆心在原点O,半径为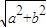 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为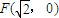 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为 .
.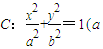 >b>0),称圆心在原点O,半径为
>b>0),称圆心在原点O,半径为 的圆是椭圆C的“伴随圆”.若椭圆C的一个焦点为
的圆是椭圆C的“伴随圆”.若椭圆C的一个焦点为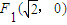 ,其短轴上的一个端点到F1的距离为
,其短轴上的一个端点到F1的距离为 .
. >b>0),称圆心在原点O,半径为
>b>0),称圆心在原点O,半径为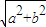 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为 .
.