题目内容
已知 的解集,若CRA是?RB的必要不充分条件;
的解集,若CRA是?RB的必要不充分条件;
求:
(Ⅰ)集合A,B;
(Ⅱ)实数m的取值范围.
解:(Ⅰ)由|1- |≤2得:-2≤
|≤2得:-2≤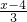 ≤2,
≤2,
∴-2≤x≤10,
∴A=[-2,10];
∵x2-2x+1-m2=[x-(1-m)][x-(1+m)]≤0,
∴当m≥0时,B=[1-m,1+m];
当m<0时,B=[1+m,1-m];
(Ⅱ)∵CRA是?RB的必要不充分条件,
∴B是A的必要不充分条件.
∴当m≥0时,A=[-2,10]⊆B=[1-m,1+m];
即
∴m≥9;
当m<0时,A=[-2,10]⊆B=[1+m,1-m];
同理可得,m≤-9.
分析:(Ⅰ)利用绝对值不等式与一元二次不等式即可求得集合A,B;
(Ⅱ)CRA是?RB的必要不充分条件?B是A的必要不充分条件,从而解不等式组即可.
点评:本题考查绝对值不等式的解法,考查必要条件、充分条件与充要条件的判断,考查分类讨论思想,属于中档题.
 |≤2得:-2≤
|≤2得:-2≤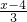 ≤2,
≤2,∴-2≤x≤10,
∴A=[-2,10];
∵x2-2x+1-m2=[x-(1-m)][x-(1+m)]≤0,
∴当m≥0时,B=[1-m,1+m];
当m<0时,B=[1+m,1-m];
(Ⅱ)∵CRA是?RB的必要不充分条件,
∴B是A的必要不充分条件.
∴当m≥0时,A=[-2,10]⊆B=[1-m,1+m];
即

∴m≥9;
当m<0时,A=[-2,10]⊆B=[1+m,1-m];
同理可得,m≤-9.
分析:(Ⅰ)利用绝对值不等式与一元二次不等式即可求得集合A,B;
(Ⅱ)CRA是?RB的必要不充分条件?B是A的必要不充分条件,从而解不等式组即可.
点评:本题考查绝对值不等式的解法,考查必要条件、充分条件与充要条件的判断,考查分类讨论思想,属于中档题.

练习册系列答案
相关题目