题目内容
离心率为黄金比 的椭圆称为“优美椭圆”.设
的椭圆称为“优美椭圆”.设
是优美椭圆,F、A分别是它的左焦点和右顶点,B是它的短轴的一个顶点,则
等于( )
A. | B. | C. | D. |
C
解析考点:椭圆的简单性质.
专题:新定义.
分析:通过 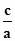 =
=  ,推出 2c2="(3-"
,推出 2c2="(3-"  )a2,验证|FA|2=|FB|2+|AB|2成立所以所以∠FBA等于 90°.
)a2,验证|FA|2=|FB|2+|AB|2成立所以所以∠FBA等于 90°.
解答:解:∵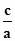 =
=
∴2c2=(3- )a2
)a2
在三角形FAB中有b2+c2=a2
|FA|=a+c,|FB|=a,|AB|=
∴|FA|2=(a+c)2=a2+c2+2ac,|FB|2+|AB|2=2a2+b2=3a2-c2
∴|FA|2=|FB|2+|AB|2= a2
a2
∴|FA|2=|FB|2+|AB|2
所以∠FBA等于 90°.
故选C.
点评:解决此类问题关键是熟练掌握椭圆的几何性质,以及利用边长关系判断三角形的形状的问题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
椭圆 上一点M到焦点
上一点M到焦点 的距离为2,
的距离为2, 是
是 的中点,
的中点,
则 等于( *** )
等于( *** )
| A.2 | B. | C. | D. |
若抛物线C:  上一点P到定点A(0,1)的距离为2, 则P到x轴的距离为( )
上一点P到定点A(0,1)的距离为2, 则P到x轴的距离为( )
| A.0 | B.1 | C.2 | D.4 |
椭圆 的准线与
的准线与 轴平行, 那么
轴平行, 那么 的取值范围为
的取值范围为
A. | B. | C. | D. |
已知 是双曲线
是双曲线 的一条渐近线,则双曲线的离心率等于
的一条渐近线,则双曲线的离心率等于
A. | B. | C. | D. |
已知双曲线 的一条渐近线方程为
的一条渐近线方程为 ,则双曲线的离心率为
,则双曲线的离心率为
A. | B. | C.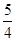 | D. |
已知椭圆 :
: 的焦点分别为
的焦点分别为 ,如果椭圆上存在点
,如果椭圆上存在点 ,使得
,使得 ·
· ,则椭圆离心率的取值范围是( )
,则椭圆离心率的取值范围是( )
A.( ] ] | B. [ ) ) | C. ( ] ] | D.[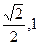 ) ) |
 的右焦点
的右焦点 ,其右准线与
,其右准线与 轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点
轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点 (B)
(B) (C)
(C)  (D)
(D)
 、
、 分别为双曲线
分别为双曲线 的左、右焦点,若在双曲线右支上存在点
的左、右焦点,若在双曲线右支上存在点 ,满足
,满足 ,且
,且 的距离等于双曲线的实轴长,则该双曲线的渐近线方程为 ( )
的距离等于双曲线的实轴长,则该双曲线的渐近线方程为 ( )


