题目内容
(本题满分12分)已知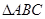 三边所在直线方程
三边所在直线方程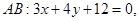
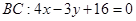 ,
,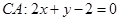 ,求
,求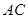 边上的高所在的直线方程.
边上的高所在的直线方程.
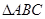 三边所在直线方程
三边所在直线方程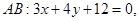
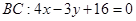 ,
,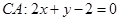 ,求
,求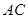 边上的高所在的直线方程.
边上的高所在的直线方程.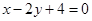
试题分析:解:由
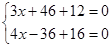 解得交点B(-4,0),
解得交点B(-4,0),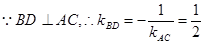 .
. ∴AC边上的高线BD的方程 为
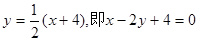 .
.点评:解决该试题的关键是利用两直线的垂直关系,得到高线所在直线的斜率,然后再利用两条直线的交点得到端点A,C的坐标一个即可,结合点斜式方程得到结论,属于基础题。体现了直线的位置关系的运用。

练习册系列答案
相关题目
题目内容
 三边所在直线方程
三边所在直线方程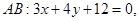
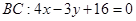 ,
,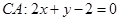 ,求
,求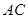 边上的高所在的直线方程.
边上的高所在的直线方程.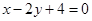
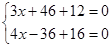 解得交点B(-4,0),
解得交点B(-4,0),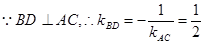 .
. 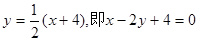 .
.