题目内容
有下列命题:①“若 ,则
,则 、
、 互为倒数”的逆命题;②“面积相等的两个三角形全等”的否命题;③“若
互为倒数”的逆命题;②“面积相等的两个三角形全等”的否命题;③“若 ,则
,则 有实数根”的逆否命题;④“若
有实数根”的逆否命题;④“若 ”的逆否命题。其中正确的是( )
”的逆否命题。其中正确的是( )
| A.①② | B.②③ | C.①②③ | D.③④ |
C
解析试题分析:由题意,①可由数的运算规则判断,②可写出它的否命题判断,③可通过判断它的原命题的真假判断逆否命题的真假,④可通过判断它的原命题的真假判断逆否命题的真假解:①命题“若xy=1,则x,y互为倒数”的逆命题;是正确命题,因为两数互为倒数,其乘积必为1;②命题“面积相等的三角形全等”的否命题;是正确命题,因为面积不相等的三角形一定不全等;③命题“若m≤1,则x2-2x+m=0有实根”的逆否命题;是正确命题,因为原命题中,m≤1可得出△≥0,故原命题真,由此知,其逆否命题也是真命题;④命题“若A∪B=B,则A⊆B”的逆否命题是正确命题,因为命题“ ”是假命题,故其逆否命题也是真命题,综上①、②、③、是真命题,故答案为C
”是假命题,故其逆否命题也是真命题,综上①、②、③、是真命题,故答案为C
考点:四种命题的关系
点评:本题考点是四种命题的关系,考查了四种命题的形式及真假的判断,解题的关键是熟练掌握四种命题的定义,及它们之间真假的对应关系,本题考察了推理判断的能力

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知命题 :“
:“


 ””是“函数
””是“函数
 的图象经过第二象限”的充分不必 要条件,命题
的图象经过第二象限”的充分不必 要条件,命题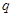 :
: ,
, 是任意实数,若a
是任意实数,若a b,则
b,则 .则
.则
A. 假 假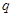 真 真 | B.“ 且 且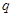 ”为真 ”为真 |
C.“ 或 或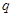 ”为真 ”为真 | D. , ,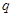 均为假命题 均为假命题 |
“ ”是“直线
”是“直线 与直线
与直线 平行”的( )条件.
平行”的( )条件.
| A.充要 | B.充分不必要 | C.必要不充分 | D.既不充分也不必要 |
“ ” 是“
” 是“ ”成立的 ( )
”成立的 ( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.非充分非必要条件 | D.充要条件 |
若 :
: ,
, ,则
,则
A. : : , , | B. : : , , |
C. : : , , | D. : : , , |
命题“存在 ”的否定是( )
”的否定是( )
A.存在 | B.不存在 |
C.对任意 | D.对任意 |
命题“若α= ,则tanα=1”的逆否命题是
,则tanα=1”的逆否命题是
A.若α≠ ,则tanα≠1 ,则tanα≠1 | B.若α= ,则tanα≠1 ,则tanα≠1 |
C.若tanα≠1,则α≠ | D.若tanα≠1,则α= |
设 ,那么“
,那么“ ”是“
”是“ ”的 ( )
”的 ( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充要条件 | D.既不充分又不必要条件 |
(5分)设x∈Z,集合A是奇数集,集合B是偶数集.若命题p:?x∈A,2x∈B,则( )
| A.¬p:?x∈A,2x∈B | B.¬p:?x∉A,2x∈B |
| C.¬p:?x∈A,2x∉B | D.¬p:?x∉A,2x∉B |