题目内容
设集合A={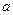 |
|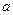 =
=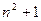 ,
,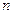 ∈N+},集合B={
∈N+},集合B={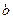 |
|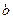 =
=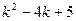 ,
,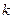 ∈N+},试证:A
∈N+},试证:A B.
B.
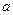 |
|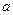 =
=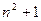 ,
,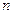 ∈N+},集合B={
∈N+},集合B={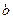 |
|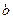 =
=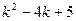 ,
,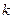 ∈N+},试证:A
∈N+},试证:A B.
B.
证明:任设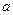 ∈A,
∈A, 
则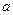 =
=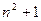 =(
=(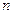 +2)2-4(
+2)2-4(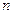 +2)+5 (
+2)+5 (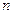 ∈N+),
∈N+),
∵ n∈N*,∴ n+2∈N*
∴ a∈B故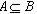 ①
①
显然,1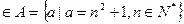 ,而由
,而由
B={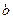 |
|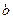 =
=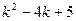 ,
,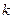 ∈N+}={
∈N+}={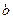 |
|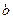 =
=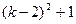 ,
,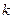 ∈N+}知1∈B,于是A≠B ②
∈N+}知1∈B,于是A≠B ②
由①、② 得A B.
B.
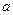 ∈A,
∈A, 
则
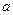 =
=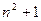 =(
=(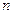 +2)2-4(
+2)2-4(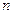 +2)+5 (
+2)+5 (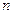 ∈N+),
∈N+),
∵ n∈N*,∴ n+2∈N*

∴ a∈B故
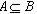 ①
①
显然,1
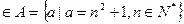 ,而由
,而由
B={
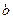 |
|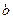 =
=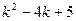 ,
,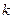 ∈N+}={
∈N+}={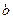 |
|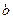 =
=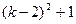 ,
,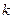 ∈N+}知1∈B,于是A≠B ②
∈N+}知1∈B,于是A≠B ②
由①、② 得A
 B.
B.(1)判定集合间的关系,其基本方法是归结为判定元素与集合之间关系.
(2)判定两集合相等,主要是根据集合相等的定义.
(2)判定两集合相等,主要是根据集合相等的定义.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
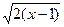 },B={x|x2–ax≤x–a},当A
},B={x|x2–ax≤x–a},当A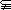 B时,则a的取值范围是 .
B时,则a的取值范围是 .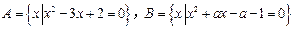 ,若
,若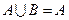 ,
,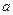 的取值。
的取值。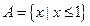 ,
, ,且
,且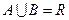 ,
,
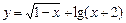 },Q={
},Q={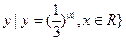 ,则P∩Q=( )
,则P∩Q=( )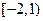
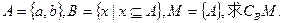
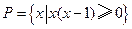 ,
,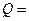
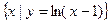 ,则
,则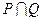 = .
= .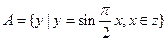 ,集合
,集合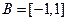 ,则
,则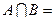 ( )
( )