题目内容
已知定义在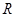 上的奇函数
上的奇函数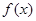 ,当
,当 时,
时,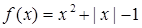 ,那么
,那么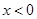 时,
时,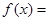 。
。
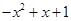
解析试题分析:任取x<0,则-x>0,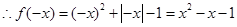 =,又
=,又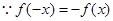 ,
,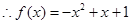
考点:本题考查分段函数的知识点,函数的性质奇偶性结合绝对值的运算.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
题目内容
已知定义在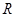 上的奇函数
上的奇函数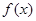 ,当
,当 时,
时,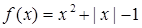 ,那么
,那么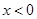 时,
时,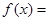 。
。
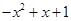
解析试题分析:任取x<0,则-x>0,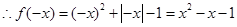 =,又
=,又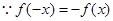 ,
,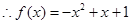
考点:本题考查分段函数的知识点,函数的性质奇偶性结合绝对值的运算.

 计算高手系列答案
计算高手系列答案