题目内容
已知函数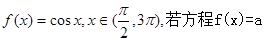 有三个不同的根,则“三个根从小到大依次成等比数列”是“
有三个不同的根,则“三个根从小到大依次成等比数列”是“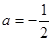 ”的 ( )
”的 ( )
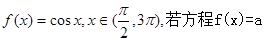 有三个不同的根,则“三个根从小到大依次成等比数列”是“
有三个不同的根,则“三个根从小到大依次成等比数列”是“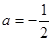 ”的 ( )
”的 ( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充分且必要条件 | D.既不充分也不必要条件 |
C
首先画图分析求出a的范围,再由三个根从小到大依次成等比数列判断出a只有一个根,而a=-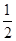 正好满足条件,故a=-
正好满足条件,故a=-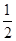 即为唯一解,故应为充分且必要条件.
即为唯一解,故应为充分且必要条件.
解答:解:
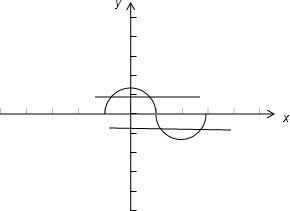
∵经画图知要使满足f(x)=a在(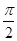 ,3π)有三个不同的根
,3π)有三个不同的根
∴则必有-1<a<0
又∵三个根从小到大依次成等比数列
∴a只有一个值
当a=-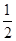 时,知f(x)=a的三个根分别为
时,知f(x)=a的三个根分别为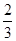 π,
π,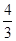 π,
π,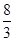 π
π
易知三个根从小到大依次成等比数列
即得a=-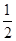 .
.
故选C.
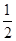 正好满足条件,故a=-
正好满足条件,故a=-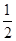 即为唯一解,故应为充分且必要条件.
即为唯一解,故应为充分且必要条件.解答:解:

∵经画图知要使满足f(x)=a在(
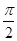 ,3π)有三个不同的根
,3π)有三个不同的根∴则必有-1<a<0
又∵三个根从小到大依次成等比数列
∴a只有一个值
当a=-
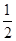 时,知f(x)=a的三个根分别为
时,知f(x)=a的三个根分别为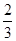 π,
π,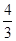 π,
π,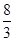 π
π易知三个根从小到大依次成等比数列
即得a=-
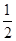 .
.故选C.

练习册系列答案
相关题目
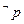 是
是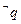 的必要不充分条件,求实数a的去值范围.
的必要不充分条件,求实数a的去值范围.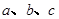 是直线,
是直线,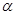 是平面,
是平面,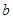 、
、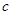
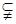
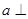 平面
平面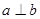 且
且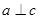 ”
”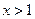 ,
,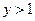 ,条件q:
,条件q: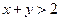 ,
,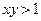 ,则条件p是条件q的 ( )
,则条件p是条件q的 ( )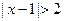 ,命题乙:
,命题乙: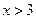 ,则甲是乙的( ).
,则甲是乙的( ). ,那么“
,那么“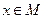 ,或
,或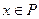 ”是“
”是“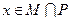 ”的( )
”的( ) 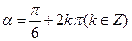 ”是“
”是“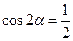 ”的 条件。
”的 条件。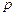 :
: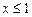 ,条件
,条件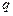 :
: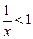 ,则
,则