��Ŀ����
 ��ͼ������������ת�̣�A������B����������ͼ���������������Բ�ĽǷֱ�Ϊ60�㡢120�㡢180�㣮��������ת�̽�������Ϸ�������ǣ�ͬʱת������ת�̴�ָ��ͣ�£�������ת��������һ��ָ��ǡ�����ڷֽ���ʱ�������ת����Ч�����¿�ʼ������ת�̣�A��ָ�����Ե�������Ϊx��ת�̣�B��ָ�����Ե�����Ϊy��x��y��{1��2��3}����x+y��ֵΪ�Σ�ÿһ����Ϸ�õ�������Ϊ��
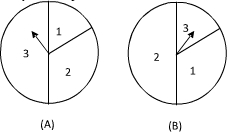
��ͼ������������ת�̣�A������B����������ͼ���������������Բ�ĽǷֱ�Ϊ60�㡢120�㡢180�㣮��������ת�̽�������Ϸ�������ǣ�ͬʱת������ת�̴�ָ��ͣ�£�������ת��������һ��ָ��ǡ�����ڷֽ���ʱ�������ת����Ч�����¿�ʼ������ת�̣�A��ָ�����Ե�������Ϊx��ת�̣�B��ָ�����Ե�����Ϊy��x��y��{1��2��3}����x+y��ֵΪ�Σ�ÿһ����Ϸ�õ�������Ϊ����1����x��2��y��1�ĸ��ʣ�
��2��ij�˽�����12����Ϸ������ƽ�����Եõ��Ľ����֣�
��������1��������ͼ���������������Բ�ĽǷֱ�Ϊ60�㡢120�㡢180�㣬����Բ�ĽǶ��������x��yȡ��ֵͬʱ�ĸ��ʣ����ݻ����¼��ĸ���������ۣ�
��2����������֪�ε�ȡֵΪ��2��3��4��5��6������=2ʱ����x=1��y=1�����ݶ����¼�ͬʱ�����ĸ��������������ͬ���ķ��������������ֵ��Ӧ�ĸ��ʣ�д���ֲ��к�����������ƽ�����Եõ��Ľ����֣�
��2����������֪�ε�ȡֵΪ��2��3��4��5��6������=2ʱ����x=1��y=1�����ݶ����¼�ͬʱ�����ĸ��������������ͬ���ķ��������������ֵ��Ӧ�ĸ��ʣ�д���ֲ��к�����������ƽ�����Եõ��Ľ����֣�
����⣺��1���ɼ��θ���ģ�Ϳ�֪��
P(x=1)=
��P(x=2)=
��P(x=3)=
��
P(y=1)=
��P(y=2)=
��P(y=3)=
��P(x��2)=P(x=1)=
��P(y��1)=P(y=2)+p(y=3)=
��
��P(x��2��y��1)=P(x��2)•P(y��1)=
��2����������֪�ε�ȡֵΪ��2��3��4��5��6��
����=2ʱ����x=1��y=1��P����=2��=P��x=1��P��y=1��=
��
��ͬ���ķ��������������ֵ��Ӧ�ĸ���
P����=3��=
��P����=4��=
��P����=5��=
��P����=6��=
��εķֲ���Ϊ��
��ƽ��һ�εõ��Ľ����ּ�Ϊ�ε�����ֵ��E��=2��
+3��
+4��
+5��
+6��
=
��
�������12��ƽ�����Եõ�12•E��=50
P(x=1)=
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
P(y=1)=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
��P(x��2)=P(x=1)=
| 1 |
| 6 |
| 2 |
| 3 |
��P(x��2��y��1)=P(x��2)•P(y��1)=
| 1 |
| 9 |
��2����������֪�ε�ȡֵΪ��2��3��4��5��6��
����=2ʱ����x=1��y=1��P����=2��=P��x=1��P��y=1��=
| 1 |
| 18 |
��ͬ���ķ��������������ֵ��Ӧ�ĸ���
P����=3��=
| 7 |
| 36 |
| 13 |
| 36 |
| 11 |
| 36 |
| 3 |
| 36 |
��εķֲ���Ϊ��
| �� | 2 | 3 | 4 | 5 | 6 | ||||||||||
| P |
|
|
|
|
|
| 1 |
| 18 |
| 7 |
| 36 |
| 13 |
| 36 |
| 11 |
| 36 |
| 1 |
| 12 |
| 25 |
| 6 |
�������12��ƽ�����Եõ�12•E��=50
�������������ø���֪ʶ���ʵ�������������ע����������ظ����������������������жϸ��ʵ��������ѵ�Ҳ���ص㣬������Ŀ�߿��ؿ���Ӧע�����ĸ�ʽ��

��ϰ��ϵ�д�
 ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д�
�����Ŀ
|
������![]() ������
������![]() �����ĸ��ʣ�
�����ĸ��ʣ�
����ij�˽�����12����Ϸ������ƽ�����Եõ��Ľ�����.
 ��2010•�麣��ģ����ͼ������������ת�̣�A������B����������ͼ�е��ĸ����������Բ�ĽǷֱ�Ϊ60�㡢120�㡢90��90�㣮��������ת�̽�������Ϸ�������ǣ�ͬʱת������ת�̴�ָ��ͣ�£�������ת��������һ��ָ��ǡ�����ڷֽ���ʱ�������ת����Ч�����¿�ʼ������ת�̣�A��ָ�����Ե�������Ϊx��ת�̣�B��ָ�����Ե�������Ϊy��x��y��{1��2��3��4}����x+y��ֵΪ�Σ�ÿһ����Ϸ�õ�������Ϊ�Σ�
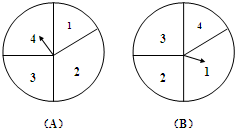
��2010•�麣��ģ����ͼ������������ת�̣�A������B����������ͼ�е��ĸ����������Բ�ĽǷֱ�Ϊ60�㡢120�㡢90��90�㣮��������ת�̽�������Ϸ�������ǣ�ͬʱת������ת�̴�ָ��ͣ�£�������ת��������һ��ָ��ǡ�����ڷֽ���ʱ�������ת����Ч�����¿�ʼ������ת�̣�A��ָ�����Ե�������Ϊx��ת�̣�B��ָ�����Ե�������Ϊy��x��y��{1��2��3��4}����x+y��ֵΪ�Σ�ÿһ����Ϸ�õ�������Ϊ�Σ�
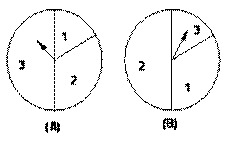
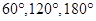 ����������ת�̽�����Ϸ�������ǣ�ͬʱת������ת�̴�ָ��ͣ�£�������ת��������һ��ָ��ǡ�����ڷֽ���ʱ�������ת����Ч�����¿�ʼ������ת�̣�A��ָ�����Ե�����Ϊx��ת�̣�B��ָ�����Ե�����Ϊy��
����������ת�̽�����Ϸ�������ǣ�ͬʱת������ת�̴�ָ��ͣ�£�������ת��������һ��ָ��ǡ�����ڷֽ���ʱ�������ת����Ч�����¿�ʼ������ת�̣�A��ָ�����Ե�����Ϊx��ת�̣�B��ָ�����Ե�����Ϊy��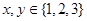 ����
����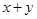 ��ֵΪ
��ֵΪ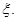
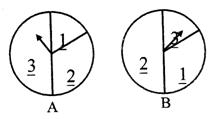
 �ĸ��ʣ�
�ĸ��ʣ� �ķ���������ѧ������
�ķ���������ѧ������