题目内容
三名学生与两名老师并排站成一排。如果老师甲必须排在老师乙的左边,且两名老师必须相邻,那么不同的排法共有( )种.
| A.60 | B.48 | C.36 | D.24 |
D
解析试题分析:必须相邻可以采用捆绑法,把两个老师捆绑在一起看作一个元素,然后与三个学生全排列即可.
考点:捆绑法解排列组合问题.

练习册系列答案
相关题目
甲、乙两人从4门课程中各选修1门,则甲、乙所选的课程不相同的选法共有 ( )
| A.6种 | B.12种 | C.30种 | D.36种 |
若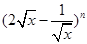 展开式中所有项的二项式系数之和为64,则展开式中含
展开式中所有项的二项式系数之和为64,则展开式中含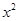 项的系数是( )
项的系数是( )
| A.192 | B.182 | C.-192 | D.-182 |
 展开式中的常数项为( )
展开式中的常数项为( )
A.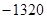 | B.1320 | C.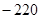 | D.220 |
已知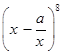 展开式中常数项为5670,其中
展开式中常数项为5670,其中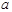 是常数,则展开式中各项系数的和是( )
是常数,则展开式中各项系数的和是( )
| A.28 | B.48 | C.28或48 | D.1或28 |
已知(x-m)7=a0+a1x+a2x2+…+a7x7的展开式中x5的系数是189,则实数m=( )
| A.3 | B.-3 | C.±3 | D.5 |
用0,1,2,3,4这五个数字组成无重复数字的五位数,其中恰有一个偶数数字夹在两个奇数数字之间,这样的五位数有( )
| A.48个 | B.12个 | C.36个 | D.28个 |
若(3x+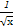 )n的展开式中各项系数的和为1024,则展开式中含x的整数次幂的项共有( )
)n的展开式中各项系数的和为1024,则展开式中含x的整数次幂的项共有( )
| A.2项 | B.3项 | C.5项 | D.6项 |
将字母a,a,b,b,c,c排成三行两列,要求每行的字母互不相同,每列的字母也互不相同,则不同的排列方法共有( )
| A.12种 | B.18种 | C.24种 | D.36种 |