题目内容
在直角坐标系中以原点O为极点,x轴的正半轴为极轴建立极坐标系,且在两种坐标系中取相同的长度单位.已知圆C的圆心的极坐标C(1,
),半径r=1,直线l的参数方程为
(t为参数).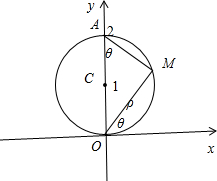
(1)求圆的极坐标方程,并将极坐标方程化成直角坐标方程;
(2)将直线l的参数方程化为普通方程,并判断直线l与圆C的位置关系.
| π |
| 2 |
|

(1)求圆的极坐标方程,并将极坐标方程化成直角坐标方程;
(2)将直线l的参数方程化为普通方程,并判断直线l与圆C的位置关系.
分析:(1)设圆C上任意一点为M(ρ,θ),A(2,
).如图所示,利用切线的性质可得∠OAM=θ.在Rt△OMA中,OA=2,利用直角三角形的边角关系MO=AOsinθ.即可得出.
(2)两式相减即可消去参数t可得直线l的普通方程,由于直线l过圆内一点即可得到直线与圆的位置关系.
| π |
| 2 |
(2)两式相减即可消去参数t可得直线l的普通方程,由于直线l过圆内一点即可得到直线与圆的位置关系.
解答:解:(1)设圆C上任意一点为M(ρ,θ),A(2,
).如图所示,
在Rt△OMA中,OA=2,由MO=AOsinθ得ρ=2sinθ.
化为直角坐标方程x2+(y-1)2=1.(或x2+y2-2y=0.)
(2)由直线l的参数方程为
(t为参数).消去参数t可得x-1=y-2,得直线l的普通方程x-y+1=0.
∵圆心C(0,1)满足直线l的方程,
∴直线与圆C相交.
| π |
| 2 |

在Rt△OMA中,OA=2,由MO=AOsinθ得ρ=2sinθ.
化为直角坐标方程x2+(y-1)2=1.(或x2+y2-2y=0.)
(2)由直线l的参数方程为
|
∵圆心C(0,1)满足直线l的方程,
∴直线与圆C相交.
点评:熟练掌握直线圆相切的性质、极坐标方程化为直角坐标方程的公式、直线与圆的位置公式的判定方法等是解题的关键.

练习册系列答案
相关题目
 中,以原点
中,以原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系.曲线
轴的正半轴为极轴建立极坐标系.曲线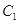 的参数方程为
的参数方程为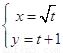 (
(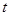 为参数),曲线
为参数),曲线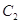 的极坐标方程为
的极坐标方程为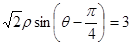 ,则
,则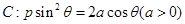 过点P(-2,-4)的直线
过点P(-2,-4)的直线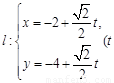 为参数)与曲线C相交于点M,N两点.
为参数)与曲线C相交于点M,N两点.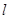 的普通方程;
的普通方程; 过点P(-2,-4)的直线
过点P(-2,-4)的直线 为参数)与曲线C相交于点M,N两点.
为参数)与曲线C相交于点M,N两点. 的普通方程;
的普通方程; 轴的正半轴为极轴建坐标系,已知曲线
轴的正半轴为极轴建坐标系,已知曲线 ,已知过点
,已知过点 的直线
的直线 的参数方程为:
的参数方程为: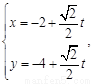 直线
直线 分别交于
分别交于
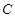 和直线
和直线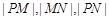 成等比数列,求
成等比数列,求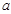 的值.
的值.