题目内容
某种电子玩具按下按钮后,会出现红球或绿球,已知按钮第一次按下后,出现红球与绿球的概率都是 ,从按钮第二次按下起,若前次出现红球,则下一次出现红球、绿球的概率分别为
,从按钮第二次按下起,若前次出现红球,则下一次出现红球、绿球的概率分别为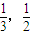 ;若前次出现绿球,则下一次出现红球、绿球的概率分别为
;若前次出现绿球,则下一次出现红球、绿球的概率分别为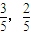 ,记第n次按下按钮后出现红球的概率为Pn.
,记第n次按下按钮后出现红球的概率为Pn.(1)求P2的值;
(2)当n∈N*,n≥2时,
①求用Pn-1表示Pn的表达式;
②求Pn关于n的表达式.
【答案】分析:(1)先求出第一次,第二次均出现红球,则概率为: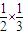 ,第一次出现绿球,第二次出现红球的概率为:
,第一次出现绿球,第二次出现红球的概率为: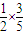 ,相加即得所求.
,相加即得所求.
(2)①设第n-1次按下按钮出现红球的概率为:Pn-1,n∈N,n≥2,可得 出现绿球的概率为:1-Pn-1 ,则由题意可得Pn= +
+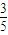 (1-Pn-1 )化简求得结果.
(1-Pn-1 )化简求得结果.
②设 Pn+x=- (Pn-1+x),即 Pn=-
(Pn-1+x),即 Pn=-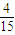 Pn-1-
Pn-1-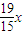 . 令-
. 令-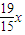 =
=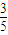 ,解得 x=
,解得 x=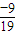 ,故Pn-
,故Pn-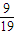 =-
=-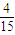 (Pn-1-
(Pn-1-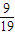 ),故{ Pn-
),故{ Pn-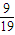 }是等比数列,首项等于
}是等比数列,首项等于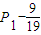 =
=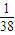 ,公比等于-
,公比等于-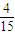 ,由此求得Pn关于n的表达式.
,由此求得Pn关于n的表达式.
解答:解:(1)P2是“第二次按下按钮后出现红球”.
若第一次,第二次均出现红球,则概率为: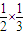 =
= ,
,
第一次出现绿球,第二次出现红球的概率为: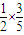 =
=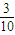 ,
,
故所求概率为:P2= +
+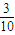 =
=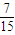 .
.
(2)①设第n-1次按下按钮出现红球的概率为:Pn-1,n∈N,n≥2,则出现绿球的概率为:1-Pn-1.
若第n-1次,第n次均出现红球,其概率为: ,
,
若第n-1次,第n次依次出现绿球,红球,其概率为:(1-Pn-1)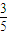 ,
,
∴Pn= +
+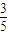 (1-Pn-1 )=
(1-Pn-1 )= -
-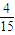 Pn-1,即Pn=
Pn-1,即Pn=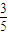 -
-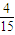 Pn-1,n∈N,n≥2.
Pn-1,n∈N,n≥2.
②设 Pn+x=-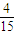 (Pn-1+x),即 Pn=-
(Pn-1+x),即 Pn=-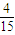 Pn-1-
Pn-1-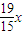 .
.
令-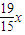 =
=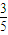 ,解得 x=
,解得 x=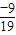 ,∴Pn-
,∴Pn-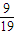 =-
=-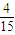 (Pn-1-
(Pn-1-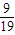 ),
),
故{ Pn-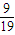 }是等比数列,首项等于
}是等比数列,首项等于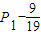 =
=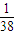 ,公比等于-
,公比等于-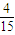 .
.
∴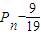 =
=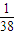
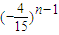 ,∴Pn=
,∴Pn=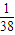
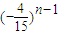 +
+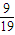 .
.
点评:本题主要考查相互独立事件的概率,互斥事件的概率加法公式的应用,等比关系的确定,等比数列的通项公式,属于中档题.
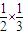 ,第一次出现绿球,第二次出现红球的概率为:
,第一次出现绿球,第二次出现红球的概率为: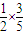 ,相加即得所求.
,相加即得所求.(2)①设第n-1次按下按钮出现红球的概率为:Pn-1,n∈N,n≥2,可得 出现绿球的概率为:1-Pn-1 ,则由题意可得Pn=
 +
+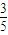 (1-Pn-1 )化简求得结果.
(1-Pn-1 )化简求得结果.②设 Pn+x=-
 (Pn-1+x),即 Pn=-
(Pn-1+x),即 Pn=-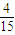 Pn-1-
Pn-1-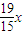 . 令-
. 令-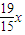 =
=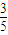 ,解得 x=
,解得 x=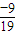 ,故Pn-
,故Pn-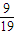 =-
=-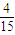 (Pn-1-
(Pn-1-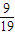 ),故{ Pn-
),故{ Pn-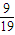 }是等比数列,首项等于
}是等比数列,首项等于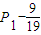 =
=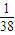 ,公比等于-
,公比等于-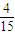 ,由此求得Pn关于n的表达式.
,由此求得Pn关于n的表达式.解答:解:(1)P2是“第二次按下按钮后出现红球”.
若第一次,第二次均出现红球,则概率为:
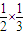 =
= ,
,第一次出现绿球,第二次出现红球的概率为:
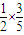 =
=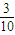 ,
,故所求概率为:P2=
 +
+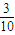 =
=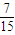 .
.(2)①设第n-1次按下按钮出现红球的概率为:Pn-1,n∈N,n≥2,则出现绿球的概率为:1-Pn-1.
若第n-1次,第n次均出现红球,其概率为:
 ,
,若第n-1次,第n次依次出现绿球,红球,其概率为:(1-Pn-1)
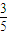 ,
,∴Pn=
 +
+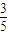 (1-Pn-1 )=
(1-Pn-1 )= -
-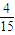 Pn-1,即Pn=
Pn-1,即Pn=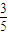 -
-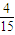 Pn-1,n∈N,n≥2.
Pn-1,n∈N,n≥2.②设 Pn+x=-
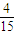 (Pn-1+x),即 Pn=-
(Pn-1+x),即 Pn=-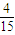 Pn-1-
Pn-1-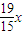 .
.令-
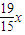 =
=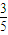 ,解得 x=
,解得 x=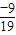 ,∴Pn-
,∴Pn-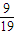 =-
=-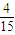 (Pn-1-
(Pn-1-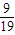 ),
),故{ Pn-
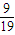 }是等比数列,首项等于
}是等比数列,首项等于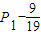 =
=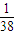 ,公比等于-
,公比等于-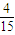 .
.∴
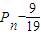 =
=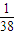
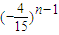 ,∴Pn=
,∴Pn=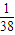
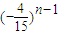 +
+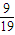 .
.点评:本题主要考查相互独立事件的概率,互斥事件的概率加法公式的应用,等比关系的确定,等比数列的通项公式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,从按钮第二次按下起,若前次出现红球,则下一次出现红球、绿球的概率分别为
,从按钮第二次按下起,若前次出现红球,则下一次出现红球、绿球的概率分别为 ;若前次出现绿球,则下一次出现红球、绿球的概率分别为
;若前次出现绿球,则下一次出现红球、绿球的概率分别为 ,记第n次按下按钮后出现红球的概率为Pn.
,记第n次按下按钮后出现红球的概率为Pn.