题目内容
某中学有5名报考艺术类的考生要参加专业測试,已知每位考生专业测试合格的概率等于| 2 |
| 3 |
(I )假设该中学5名考生恰有r人专业測试合格的概率等于
| 80 |
| 243 |
(II)假设该中学5名考生专业測试合格的人数为ξ,求ξ的期望和方差.
分析:(Ⅰ)由每位考生专业测试合格的概率求得:每位考生专业测试不合格的概率,再结合n次独立重复试验中恰好发生k次的概率即可求得该中学5名考生恰有r人专业測试合格的概率,列出方程即可求得r值;
(Ⅱ)根据题意,易得 ξ:ξ~B(5,
),根据其概率分布列,由期望的计算公式,结合分布列计算可得ξ的期望和方差.
(Ⅱ)根据题意,易得 ξ:ξ~B(5,
| 2 |
| 3 |
解答:解:(I)∵每位考生专业测试合格的概率等于
.
∴每位考生专业测试不合格的概率等于1-
=
.
∴该中学5名考生恰有r人专业測试合格的概率
=c5Rpr(1-p)5-r=
?r=3,4.
(II)∵该中学5名考生专业測试合格的人数为ξ:
ξ~B(5,
)
∴ξ的期望=5×
=
方差=5×
×
=
.
| 2 |
| 3 |
∴每位考生专业测试不合格的概率等于1-
| 2 |
| 3 |
| 1 |
| 3 |
∴该中学5名考生恰有r人专业測试合格的概率
=c5Rpr(1-p)5-r=
| 80 |
| 243 |
(II)∵该中学5名考生专业測试合格的人数为ξ:
ξ~B(5,
| 2 |
| 3 |
∴ξ的期望=5×
| 2 |
| 3 |
| 10 |
| 3 |
方差=5×
| 2 |
| 3 |
| 1 |
| 3 |
| 10 |
| 9 |
点评:本题考查对立事件、n次独立重复试验中恰好发生k次的概率计算与由分布列求期望的方法,关键是明确事件之间的关系,准确得出概率的类型.

练习册系列答案
相关题目
 .
. ,求r的值;
,求r的值; .
.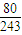 ,求r的值;
,求r的值; .
. ,求r的值.
,求r的值.