题目内容
已知y=asinx+
sin3x在x=
处有极值，则（ ）
| 1 |
| 3 |
| π |
| 3 |
分析：求导函数，利用y=asinx+
sin3x在x=
处有极值，可得x=
时，y′=acos
+cosπ=0，从而可求a的值．
| 1 |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
解答：解：求导函数，可得y′=acosx+cos3x
∵y=asinx+
sin3x在x=
处有极值，
∴x=
时，y′=acos
+cosπ=0
∴a=2
故选B．
∵y=asinx+
| 1 |
| 3 |
| π |
| 3 |
∴x=
| π |
| 3 |
| π |
| 3 |
∴a=2
故选B．
点评：本题考查导数知识的运用，考查函数的极值，解题的关键是利用函数取极值时，导数等于0．
练习册系列答案
全能测控期末小状元系列答案
相关题目
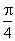，则直线ax－by＋c＝0的倾斜角为
