题目内容
定义在 上的函数
上的函数 对任意
对任意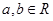 都有
都有 (
(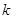 为常数).
为常数).
(1)判断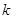 为何值时
为何值时 为奇函数,并证明;
为奇函数,并证明;
(2)设 ,
, 是
是 上的增函数,且
上的增函数,且 ,若不等式
,若不等式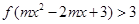 对任意
对任意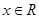 恒成立,求实数
恒成立,求实数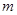 的取值范围.
的取值范围.
【答案】
(1)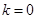 ,证明过程详见解析;(2)
,证明过程详见解析;(2)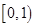 .
.
【解析】
试题分析:本题主要考查抽象函数奇偶性的判断和利用函数单调性解不等式.考查学生的分析问题解决问题的能力.考查转化思想和分类讨论思想.第一问,用赋值法证明函数的奇偶性;第二问,利用单调性解不等式,转化成恒成立问题,再利用二次函数的性质求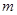 的取值范围.
的取值范围.
试题解析:(Ⅰ)若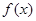 在
在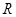 上为奇函数,则
上为奇函数,则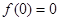 ,
1分
,
1分
令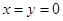 ,则
,则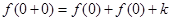 ,∴
,∴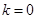 . 2分
. 2分
证明:由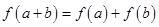 ,令
,令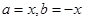 ,则
,则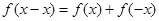 ,
,
又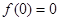 ,则有
,则有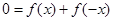 .即
.即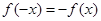 对任意
对任意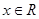 成立,所以
成立,所以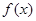 是奇函数.
是奇函数.
6分
(Ⅱ)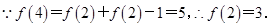 7分
7分
∴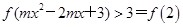 对任意
对任意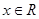 恒成立.
恒成立.
又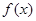 是
是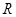 上的增函数,∴
上的增函数,∴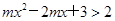 对任意
对任意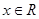 恒成立, 9分
恒成立, 9分
即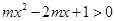 对任意
对任意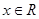 恒成立,
恒成立,
当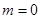 时显然成立;
时显然成立;
当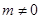 时,由
时,由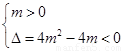 得
得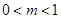 .
.
所以实数m的取值范围是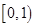 . 13分
. 13分
考点:1.抽象函数的奇偶性的判断;2.恒成立问题.

练习册系列答案
相关题目
 上的函数
上的函数 对任意实数
对任意实数 满足
满足 ,且
,且 ,则
,则 的值为(
)
的值为(
) C.0 D.4
C.0 D.4 上的函数
上的函数 对任意实数
对任意实数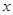 满足
满足 与
与 ,且当
,且当 时,
时, ,则( )
,则( ) B.
B.
 D.
D.
 上的函数
上的函数 对任意实数
对任意实数 满足
满足 与
与 ,且当
,且当 时,
时, ,则 ( )
,则 ( ) B.
B.
 D.
D.
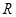 上的函数
上的函数 对任意实数
对任意实数 满足
满足 与
与 ,且当
,且当 时,
时, ,则 ( )
,则 ( ) B.
B.
 D.
D.
 上的函数
上的函数 对任意
对任意 满足
满足
 上的图像如图所示,则
上的图像如图所示,则 =
= A.3
B.2 C.1 D.0
A.3
B.2 C.1 D.0