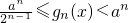题目内容
我们把y=xm(m∈Q)叫做幂函数.幂函数y=xm(m∈Q)的一个性质是:当m>0时,在(0,+∞)上是增函数;当m<0时,在(0,+∞)上是减函数.设幂函数f(x)=xn(n≥2,n∈N).(1)若gn(x)=f(x)+f(a-x),x∈(0,a),证明:
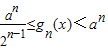
(2)若gn(x)=f(x)-f(x-a),对任意n≥a>0,证明:gn′(n)≥n!a.
【答案】分析:(1)由已知求gn(x)的值域,首先求gn′(x),在利用gn′(x)>0,gn′(x)<0分别求出函数的单调递增区间和单调递减区间,得到函数的极值点x=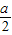 ,进而得到函数的最值,即可以得到函数的值域.
,进而得到函数的最值,即可以得到函数的值域.
(2)当x≥a>0时,gn′(x)=n[xn-1-(x-a)n-1]>0,gn(x)是关于x的增函数,当n≥a时,得(n+1)n-(n+1-a)n>nn-(n-a)n.
进而得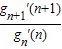 >n+1,(*),根据(*)式可以构造等式gn′(n)=
>n+1,(*),根据(*)式可以构造等式gn′(n)=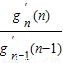 •
•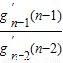 …
…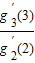 •g2′(2)>n×(n-1)×…×3×2a=n!a,又g2′(2)=2[22-1-(2-a)2-1]=2!a,故n≥2,n∈N时,有gn′(n)≥n!a
•g2′(2)>n×(n-1)×…×3×2a=n!a,又g2′(2)=2[22-1-(2-a)2-1]=2!a,故n≥2,n∈N时,有gn′(n)≥n!a
解答:证明(1)∵gn(x)=f(x)+f(a-x)=xn+(a-x)n,
∴gn′(x)=nxn-1+n(a-x)n-1(-1)=n[xn-1-(a-x)n-1]
令gn′(x)=0,得xn-1=(a-x)n-1,又x∈(0,a).
根据幂函数的单调性,得x=a-x,即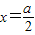 ,由下表:
,由下表:
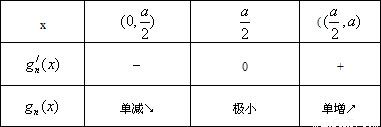
∴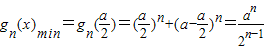
又gn(x)在x=0,x=a处连续,且gn(0)=gn(a)=an,
故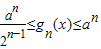 .
.
(2)∵gn(x)=f(x)-f(x-a)=xn-(x-a)n,
∴gn′(x)=n[xn-1-(x-a)n-1],
∵当x≥a>0时,gn′(x)>0,∴x≥a>0时,gn(x)是关于x的增函数,
∴当n≥a时,(n+1)n-(n+1-a)n>nn-(n-a)n.
∴gn+1′(n+1)=(n+1)[(n+1)n-(n+1-a)n]>(n+1)[nn-(n-a)n]>(n+1)[nn-n(n-a)n-1]
=(n+1)n[nn-1-(n-a)n-1]=(n+1)gn′(n)
于是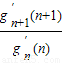 >n+1,而g2′(2)=2[22-1-(2-a)2-1]=2a
>n+1,而g2′(2)=2[22-1-(2-a)2-1]=2a
当n≥3时,gn′(n)= •
•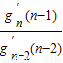 …
…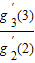 •g2′(2)>n×(n-1)×…×3×2a=n!a,
•g2′(2)>n×(n-1)×…×3×2a=n!a,
又n=2时,g2′(2)=2[22-1-(2-a)2-1]=2!a
故n≥2,n∈N时,有gn′(n)≥n!a
点评:本题主要考查函数的单调性、极值、最值等基本的函数知识,对(2)最关键的地方,是善于观察,结合平时的总结经验,构造等式gn′(n)= •
•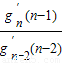 …
…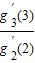 •g2′(2),进而得到结果.这道题的结论中出现n!,这时我们要能够想到构造类似的等式,这都是平时的总结经验,只有平时多总结、探索,才能在实战中,做到举一反三.
•g2′(2),进而得到结果.这道题的结论中出现n!,这时我们要能够想到构造类似的等式,这都是平时的总结经验,只有平时多总结、探索,才能在实战中,做到举一反三.
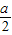 ,进而得到函数的最值,即可以得到函数的值域.
,进而得到函数的最值,即可以得到函数的值域.(2)当x≥a>0时,gn′(x)=n[xn-1-(x-a)n-1]>0,gn(x)是关于x的增函数,当n≥a时,得(n+1)n-(n+1-a)n>nn-(n-a)n.
进而得
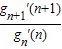 >n+1,(*),根据(*)式可以构造等式gn′(n)=
>n+1,(*),根据(*)式可以构造等式gn′(n)=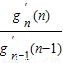 •
•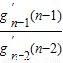 …
…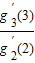 •g2′(2)>n×(n-1)×…×3×2a=n!a,又g2′(2)=2[22-1-(2-a)2-1]=2!a,故n≥2,n∈N时,有gn′(n)≥n!a
•g2′(2)>n×(n-1)×…×3×2a=n!a,又g2′(2)=2[22-1-(2-a)2-1]=2!a,故n≥2,n∈N时,有gn′(n)≥n!a解答:证明(1)∵gn(x)=f(x)+f(a-x)=xn+(a-x)n,
∴gn′(x)=nxn-1+n(a-x)n-1(-1)=n[xn-1-(a-x)n-1]
令gn′(x)=0,得xn-1=(a-x)n-1,又x∈(0,a).
根据幂函数的单调性,得x=a-x,即
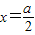 ,由下表:
,由下表:
∴
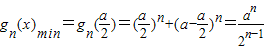
又gn(x)在x=0,x=a处连续,且gn(0)=gn(a)=an,
故
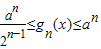 .
.(2)∵gn(x)=f(x)-f(x-a)=xn-(x-a)n,
∴gn′(x)=n[xn-1-(x-a)n-1],
∵当x≥a>0时,gn′(x)>0,∴x≥a>0时,gn(x)是关于x的增函数,
∴当n≥a时,(n+1)n-(n+1-a)n>nn-(n-a)n.
∴gn+1′(n+1)=(n+1)[(n+1)n-(n+1-a)n]>(n+1)[nn-(n-a)n]>(n+1)[nn-n(n-a)n-1]
=(n+1)n[nn-1-(n-a)n-1]=(n+1)gn′(n)
于是
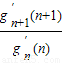 >n+1,而g2′(2)=2[22-1-(2-a)2-1]=2a
>n+1,而g2′(2)=2[22-1-(2-a)2-1]=2a当n≥3时,gn′(n)=
 •
•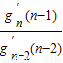 …
…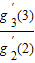 •g2′(2)>n×(n-1)×…×3×2a=n!a,
•g2′(2)>n×(n-1)×…×3×2a=n!a,又n=2时,g2′(2)=2[22-1-(2-a)2-1]=2!a
故n≥2,n∈N时,有gn′(n)≥n!a
点评:本题主要考查函数的单调性、极值、最值等基本的函数知识,对(2)最关键的地方,是善于观察,结合平时的总结经验,构造等式gn′(n)=
 •
•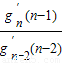 …
…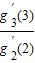 •g2′(2),进而得到结果.这道题的结论中出现n!,这时我们要能够想到构造类似的等式,这都是平时的总结经验,只有平时多总结、探索,才能在实战中,做到举一反三.
•g2′(2),进而得到结果.这道题的结论中出现n!,这时我们要能够想到构造类似的等式,这都是平时的总结经验,只有平时多总结、探索,才能在实战中,做到举一反三. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目