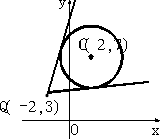Question

已知圆C：x²＋y²－4x－14y＋45＝0及点Q(－2，3)．

(1)若点P(m，m＋1)在圆C上，求直线PQ的斜率；

(2)若点M是圆C上任意一点，求|MQ|的最大值、最小值；

(3)若点N(a，b)满足关系式：a²＋b²－4a－14b＋45＝0，求t＝的最大值．

Answer 1

答案：
解析：

解：圆C的圆心(2，7)，半径长r＝2． 　　(1)因为点P(m，m＋1)在圆C上，所以m2＋(m＋1)2－4m－14(m＋1)＋45＝0，解得m＝4．故点P的坐标为(4，5)．所以直线PQ的斜率kPQ＝＝． 　　(2)点M是圆C上任意一点，点Q(－2，3)在圆外，所以|MQ|的最大值、最小值分别是|QC|＋r、|QC|－r．因为|QC|＝＝4，r＝2，所以|MQ|max＝6，|MQ|min＝2． 　　(3)由题意知，点N在圆C上，t＝表示的是定点Q(－2，3)与圆上动点N的连线l的斜率．设l的方程为y－3＝k(x＋2)，即kx－y＋2k＋3＝0，由图知，当直线和圆相切时，直线l的斜率k最大，即t最大．此时＝2，解得k＝2±．所以t＝的最大值tmax＝2＋．