题目内容
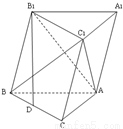
 已知斜三棱柱侧棱与底面边长均为2,侧棱与底面所成的角为60°,且侧面ABB1A1与底面垂直.
已知斜三棱柱侧棱与底面边长均为2,侧棱与底面所成的角为60°,且侧面ABB1A1与底面垂直.(1)求异面直线B1C与C1A所成的角;
(2)求此斜三棱柱的表面积.
分析:(1)取AB中点D,连结BC1,交B1C于点O,连结OD、B1D.由平行四边形形的性质和三角形中位线定理,证出∠COD(或补角)是异面直线B1C与C1A所成的角.结合题中数据算出△COD的三边之长,再利用余弦定理即可算出异面直线B1C与C1A所成的角大小;
(2)根据余弦定理解三角形,算出cos∠ACC1=-
,从而得到sin∠ACC1=
,可得S AA1C1C=
.同样的方法算出S BB1C1C=
,结合S AA1B1B=2
和S△ABC=S △A1B 1C1=
,即可求出此斜三棱柱的表面积.
(2)根据余弦定理解三角形,算出cos∠ACC1=-
| 1 |
| 4 |
| ||
| 4 |
| 15 |
| 15 |
| 3 |
| 3 |
解答:解:(1)取AB中点D,连结BC1,交B1C于点O,连结OD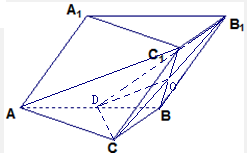 、B1D
、B1D
∵平行四边形BCC1B1的对角线交点为O,
∴O为BC1的中点,可得OD是三角形ABC1的中位线
∴OD∥AC1,∠COD(或补角)是异面直线B1C与C1A所成的角
∵平面ABC⊥侧面ABB1A1,平面ABC∩侧面ABB1A1=AB
正三角形ABC中,CD⊥AB
∴CD⊥侧面ABB1A1,
∵CD=
AB=
,B1D=
=
可得Rt△CDB1中,B1C=
=
,得C0=
=D0
∴△COD中由余弦定理,得cos∠COD=
=
因此,异面直线B1C与C1A所成的角为arccos
;
(2)由(1)得AC1=2D0=
,从而算出cos∠ACC1=
=-
∴sin∠ACC1=
,可得S AA1C1C=CC1•ACcsin∠ACC1=
同理算出S BB1C1C=
又∵S AA1B1B=A1A•ABsin60°=2
,S△ABC=S △A1B 1C1=
×22=
∴此斜三棱柱的表面积为
S=S AA1B1B+S BB1C1C+S AA1C1C+S△ABC+S △A1B 1C1=2
+4
.
 、B1D
、B1D∵平行四边形BCC1B1的对角线交点为O,
∴O为BC1的中点,可得OD是三角形ABC1的中位线
∴OD∥AC1,∠COD(或补角)是异面直线B1C与C1A所成的角
∵平面ABC⊥侧面ABB1A1,平面ABC∩侧面ABB1A1=AB
正三角形ABC中,CD⊥AB
∴CD⊥侧面ABB1A1,
∵CD=
| ||
| 2 |
| 3 |
| 1+4-2×1×2cos120° |
| 7 |
可得Rt△CDB1中,B1C=
| CD2+B 1D2 |
| 10 |
| ||
| 2 |
∴△COD中由余弦定理,得cos∠COD=
| ||||||||
2×
|
| 2 |
| 5 |
因此,异面直线B1C与C1A所成的角为arccos
| 2 |
| 5 |
(2)由(1)得AC1=2D0=
| 10 |
| 4+4-10 |
| 2×2×2 |
| 1 |
| 4 |
∴sin∠ACC1=
| ||
| 4 |
| 15 |
同理算出S BB1C1C=
| 15 |
又∵S AA1B1B=A1A•ABsin60°=2
| 3 |
| ||
| 4 |
| 3 |
∴此斜三棱柱的表面积为
S=S AA1B1B+S BB1C1C+S AA1C1C+S△ABC+S △A1B 1C1=2
| 15 |
| 3 |
点评:本题给出特殊三棱柱,求异面直线所成角大小并求该几何体表面积,着重考查了面面垂直的性质定理、正余弦定理解三角形和面积公式等知识,属于中档题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
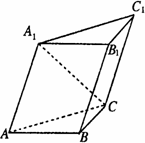
 的侧面
的侧面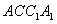 与底面ABC垂直,∠ABC=90°,BC=2,
与底面ABC垂直,∠ABC=90°,BC=2,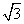 ,
,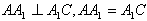 。
。 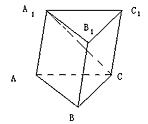
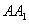 与底面ABC所成的角;
与底面ABC所成的角; 与底面ABC所成的角;
与底面ABC所成的角;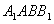 的距离。
的距离。 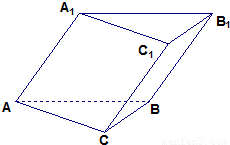
 ,且当AC=BC=AA1时,求二面角C1-AB-C的大小.
,且当AC=BC=AA1时,求二面角C1-AB-C的大小.