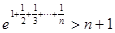题目内容
(1)求函数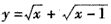 的最小值;
的最小值;
(2)已知A=[1,b](b>1),对于函数f(x)=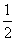 (x-1)2+1,若f(x)的定义域和值域都为A,求b的值.
(x-1)2+1,若f(x)的定义域和值域都为A,求b的值.
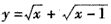 的最小值;
的最小值; (2)已知A=[1,b](b>1),对于函数f(x)=
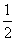 (x-1)2+1,若f(x)的定义域和值域都为A,求b的值.
(x-1)2+1,若f(x)的定义域和值域都为A,求b的值. 解:(1)由x≥0,且x-1≥0,得函数的定义域为[1,+∞),
而函数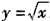 和
和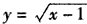 在[1,+∞)上都是增函数,
在[1,+∞)上都是增函数,
则得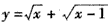 也是增函数,
也是增函数,
当x=1时,它取得最小值,所以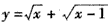 的最小值为1.
的最小值为1.
(2)函数f(x)= (x-1)2+1表示开口向上,顶点坐标是(1,1),对称轴是x=1的抛物线,
(x-1)2+1表示开口向上,顶点坐标是(1,1),对称轴是x=1的抛物线,
因此,当x∈[1,b]时,f(x)是增函数,
∴当x=b时,f(x)取最大值f(b),
故f(b)=b,即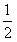 (b-1)2+1=b,
(b-1)2+1=b,
整理得b2-4b+3=0,
解得b=1或b=3,
∵b>1,
∴b=3.

练习册系列答案
相关题目
 的最小值
的最小值
 的最小值
的最小值 时,
时,
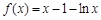
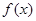 的最小值
的最小值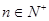 时,
时,