题目内容
某同学用“五点法”画函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<
)在某一个周期内的图象时,列表并填入的部分数据如下表:
(1)请将上表数据补全,并直接写出函数f(x)的解析式;
(2)将函数f(x)图象上各点的纵坐标不变,横坐标缩短到原来的
,得到函数y=g(x)的图象,求函数y=g(x)的单调减区间.
| π |
| 2 |
| x |
|
|
|||||||
| ωx+φ | 0 |
|
π |
|
2π | ||||
| Asin(ωx+φ) | 0 | 2 | 0 | -2 |
(2)将函数f(x)图象上各点的纵坐标不变,横坐标缩短到原来的
| 1 |
| 2 |
分析:(1)由表知,
×ω+φ=
①,
×ω+φ=
②,联立可求ω,φ,令x-
=0,π,2π可求相应的x;
(2)根据图象变换易求g(x),利用正弦函数的单调性可求得g(x)的减区间;
| 2π |
| 3 |
| π |
| 2 |
| 5π |
| 3 |
| 3π |
| 2 |
| π |
| 6 |
(2)根据图象变换易求g(x),利用正弦函数的单调性可求得g(x)的减区间;
解答:解:(1)由表知,
×ω+φ=
①,
×ω+φ=
②,联立①②解得ω=1,φ=-
,
令x-
=0,π,2π可求得x=
,
,
,填表如下:
函数f(x)的解析式为f(x)=2sin(x-
);
(2)函数g(x)=2sin(2x-
),
令2kπ+
≤2x-
≤2kπ+
,k∈Z,
得kπ+
≤x≤kπ+
,k∈Z
∴函数g(x)的单调减区间是[kπ+
,kπ+
],k∈Z;
| 2π |
| 3 |
| π |
| 2 |
| 5π |
| 3 |
| 3π |
| 2 |
| π |
| 6 |
令x-
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| 13π |
| 6 |
| x |
|
|
|
|
| ||||||||||
| ωx+φ | 0 |
|
π |
|
2π | ||||||||||
| Asin(ωx+φ) | 0 | 2 | 0 | -2 | 0 |
| π |
| 6 |
(2)函数g(x)=2sin(2x-
| π |
| 6 |
令2kπ+
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
得kπ+
| π |
| 3 |
| 5π |
| 6 |
∴函数g(x)的单调减区间是[kπ+
| π |
| 3 |
| 5π |
| 6 |
点评:本题考查“五点法”作y=Asin(ωx+φ)的图象及其图象变换、单调性,属中档题.

练习册系列答案
相关题目
某同学用“五点法”画函数y=Asin(ωx+φ)(A>0,ω>0)在一个周期内简图时,列表如下:
|
某同学用“五点法”画函数y=Asin(ωx+φ)(A>0,ω>0)在一个周期内简图时,列表如下:
则有( )
A.A=0,ω=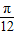 ,φ=0
,φ=0
B.A=2,ω=3,φ=
C.A=2,ω=3,φ=-
D.A=1,ω=2,φ=-
| ωx+φ |  | π |  | 2π | |
| x |  |  |  |  |  |
| y | 2 | -2 |
A.A=0,ω=
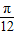 ,φ=0
,φ=0B.A=2,ω=3,φ=

C.A=2,ω=3,φ=-

D.A=1,ω=2,φ=-
