题目内容
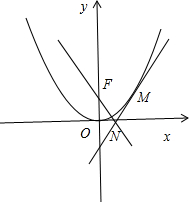
已知F为抛物线x2=ay(a>0)的焦点,O为坐标原点.点M为抛物线上的任一点,过点M作抛物线的切线交x轴于点N,设k1,k2分别为直线MO与直线NF的斜率,则k1k2=
-
| 1 |
| 2 |
-
.| 1 |
| 2 |
分析:如图所示,设M(x0,
),利用导数的运算法则可得y′=
,利用导数的聚会意义可得切线的斜率为
.利用点斜式可得过点M的抛物线的切线方程,令y=0得点N的横坐标,利用向量计算公式可得k2=kNF,k1=kMO.即可得出k1k2.
| ||
| a |
| 2x |
| a |
| 2x0 |
| a |
解答:解:如图所示,设M(x0,
),
∵y′=
,∴切线的斜率为
.
则过点M的抛物线的切线方程为:y=
(x-x0)+
,
令y=0得:xN=
x0,
可得N(
,0),F(0,
),
∴k2=kNF=-
,
又k1=kMO=
=
,
故k1k2=-
,
故答案为-
.
| ||
| a |

∵y′=
| 2x |
| a |
| 2x0 |
| a |
则过点M的抛物线的切线方程为:y=
2
| ||
| a |
| ||
| a |
令y=0得:xN=
| 1 |
| 2 |
可得N(
| x0 |
| 2 |
| a |
| 4 |
∴k2=kNF=-
| a |
| 2x0 |
又k1=kMO=
| ||||
| x0 |
| x0 |
| a |
故k1k2=-
| 1 |
| 2 |
故答案为-
| 1 |
| 2 |
点评:本题考查了直线与抛物线相切的位置关系、切线的方程、斜率的计算公式、导数的几何意义等基础知识与基本技能方法,属于中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
已知P为抛物线x2=2py(p>0)上的动点,F为抛物线的焦点,过F作抛物线在P点处的切线的垂线,垂足为G,则点G的轨迹方程为( )
| A、x2+y2=p2 | ||||
B、y=-
| ||||
C、x2+(y-
| ||||
| D、y=0 |
 已知F为抛物线C1:x2=2py(p>0)的焦点,若过焦点F的直线l交C1于A,B两点,使抛物线C1在点A,B处的两条切线的交点M恰好在圆C2:x2+y2=8上.
已知F为抛物线C1:x2=2py(p>0)的焦点,若过焦点F的直线l交C1于A,B两点,使抛物线C1在点A,B处的两条切线的交点M恰好在圆C2:x2+y2=8上.