题目内容
数列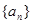 的首项
的首项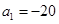 ,
,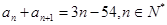
求数列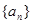 的通项公式;
的通项公式;
设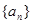 的前
的前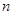 项和为
项和为 ,求
,求 的最小值.
的最小值.
(1);(2).
解析试题分析:(1)由题设递推关系,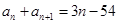 ,得
,得 ,两式相减可得
,两式相减可得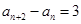 ,这说明数列
,这说明数列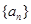 的奇数项与偶数项分别成等差数列,只要根据题意再求出
的奇数项与偶数项分别成等差数列,只要根据题意再求出 ,就能写出其通项公式;(2)由于奇数项与偶数项的表达式不相同,因此在求
,就能写出其通项公式;(2)由于奇数项与偶数项的表达式不相同,因此在求 时,要按
时,要按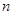 的奇偶分类讨论,当
的奇偶分类讨论,当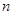 为偶数,即
为偶数,即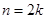 时,可求出
时,可求出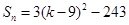
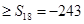 ,当
,当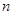 为奇数时,可求出
为奇数时,可求出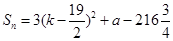 ,从而
,从而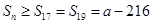 S,则题意,则应该有
S,则题意,则应该有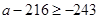 ,由此得
,由此得 的范围
的范围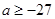 .
.
(1) +1分 又
+1分 又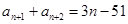 ,
,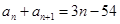
则 即奇数项成等差,偶数项成等差 +3分
即奇数项成等差,偶数项成等差 +3分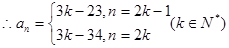 +6分 (或:
+6分 (或: 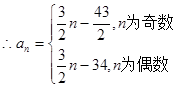 )
)
(2)当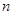 为偶数,即
为偶数,即 时:
时:
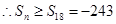 +9分
+9分
当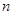 为奇数,即
为奇数,即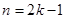 时:
时: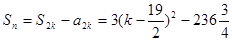
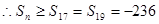 +12分
+12分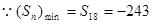 +14分
+14分
考点:(1)数列的通项公式;(2)数列的前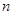 项和与最小值问题.
项和与最小值问题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
在等差数列{an}中,a2=1,a4=5,则{an}的前5项和S5=( )
| A.7 | B.15 | C.20 | D.25 |
已知等差数列 中,前n项和为
中,前n项和为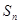 ,若
,若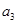 +
+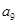 =6,则
=6,则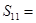 ( )
( )
| A.12 | B.33 | C.66 | D.99 |
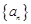 满足
满足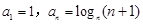
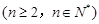 .定义:使乘积
.定义:使乘积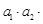 …
…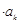 为正整数的
为正整数的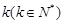 叫做“简易数”.则在
叫做“简易数”.则在 内所有“简易数”的和为 .
内所有“简易数”的和为 .  满足:
满足: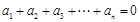 且
且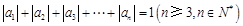 ,则称数列
,则称数列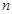 阶“归化数列”.
阶“归化数列”.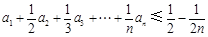 .
.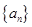 为等差数列,且
为等差数列,且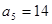 ,
,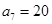 ,数列
,数列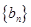 的前
的前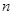 项和为
项和为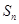 ,
,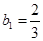 且
且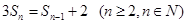 .
.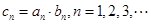 ,
,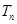 为数列
为数列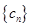 的前
的前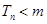 对
对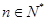 恒成立,求
恒成立,求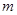 的最小值.
的最小值.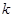 (
(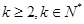 )的数列
)的数列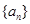 、
、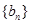 、
、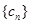 前
前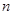 项的和分别为
项的和分别为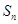 、
、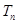 、
、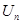 .已知集合
.已知集合 =
=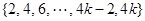 .
.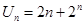 ,求数列
,求数列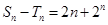
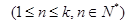 ,试研究
,试研究 和
和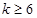 时是否存在符合条件的数列对(
时是否存在符合条件的数列对(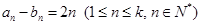 ,对于固定的
,对于固定的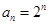 ,把数列
,把数列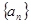 的各项排成如图所示的三角形状,记
的各项排成如图所示的三角形状,记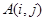 表示第i行中第j个数,则结论
表示第i行中第j个数,则结论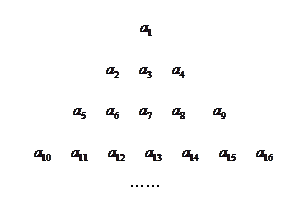
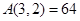 ;
;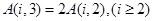 ;
;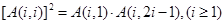 ;
;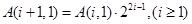 .
. 中,有
中,有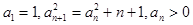 ,则通项
,则通项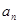 = .
= .