题目内容
已知事件A、B,则下列式子正确的是 ( )
A.P(A∪B)="P(A)+" P(B)
B.P(A)+P(B) ≥P(A∪B)
C.P(A∩B)="P(A)-" P(B)
D.P(A∩B)< P(A∪B)
B
解析试题分析:选项 A.P(A∪B)="P(A)+" P(B) 只有A,B是互斥事件的时候成立。故错误 选项B. P(A)+P(B) ≥P(A∪B),符合集合的并集的运算关系,可知概率不等式成立。
选项C.P(A∩B)="P(A)-" P(B) ,只有B是A子集时,那么成立。故错误。
选项D.P(A∩B)< P(A∪B),当A,B相等事件的时候不成立故错误。选B.
考点:本题主要考查了随机事件的概念,解题时要认真审题,注意交事件,并事件的概率的运算.
点评:解决该试题的关键是理解并事件的概率等于各自的概率和减去交事件的概率。即.P(A∪B)="P(A)+" P(B)- P(A∩B),同时利用集合的交集并集的思想来分析概率的大小问题。

练习册系列答案
相关题目
记 分别是投掷两次骰子所得的数字,则方程
分别是投掷两次骰子所得的数字,则方程 有两个不同实根的概率为( )
有两个不同实根的概率为( )
A.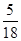 | B. | C. | D. |
从三件正品、一件次品中随机取出两件,则取出的产品全是正品的概率是( )
A.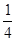 | B.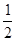 | C.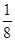 | D.无法确定 |
如果A,B是互斥事件,那么下列正确的是
A.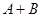 是必然事件 是必然事件 | B.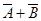 是必然事件 是必然事件 |
C.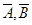 一定不互斥 一定不互斥 | D.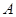 与 与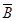 可能互斥也可能不互斥 可能互斥也可能不互斥 |
一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( )
| A.至多有一次中靶 | B.两次都中靶 |
| C.只有一次中靶 | D.两次都不中靶 |
掷两颗相同的均匀骰子(各个面分别标有1,2,3,4,5,6),记录朝上一面的两个数,那么互斥而不对立的两个事件是( )
| A.“至少有一个奇数”与“都是奇数” |
| B.“至少有一个奇数”与“至少有一个偶数” |
| C.“至少有一个奇数”与“都是偶数” |
| D.“恰好有一个奇数”与“恰好有两个奇数” |
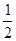 cm的正方形孔,若你随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落入孔中的概率是( )
cm的正方形孔,若你随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落入孔中的概率是( )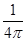
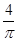
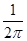
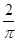
 图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为 ( )
图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为 ( )

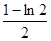

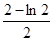
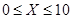 ;②
;②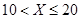 ;③
;③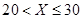 ;④
;④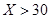 .调查了10000名中学生,下图是此次调查中某一项的流程图,其输出的结果是7300,则平均每人每周零花钱在
.调查了10000名中学生,下图是此次调查中某一项的流程图,其输出的结果是7300,则平均每人每周零花钱在 元内的学生的频率是( )
元内的学生的频率是( )