题目内容
如图，有一公共边但不共面的两个三角形ABC和A1BC被一平面DEE1D1所截，若平面DEE1D1分别交AB，AC，A1B，A1C于点D，E，D1，E1．（1）讨论这三条交线ED，CB，E1 D1的关系．
（2）当BC∥平面DEE1D1时，求
| AD |
| DB |
| BD1 |
| D1A1 |
| A1E1 |
| E1C |
| CE |
| EA |
（3）当BC不平行平面DEE1D1时，
| AD |
| DB |
| BD1 |
| D1A1 |
| A1E1 |
| E1C |
| CE |
| EA |
分析：（1）利用线面平行的性质及平行线的性质，及公理2可得结论；
（2）利用线面平行的性质及平行线的性质可得结论；
（3）利用平行线的性质，考查比例式，化简可得结论．
（2）利用线面平行的性质及平行线的性质可得结论；
（3）利用平行线的性质，考查比例式，化简可得结论．
解答：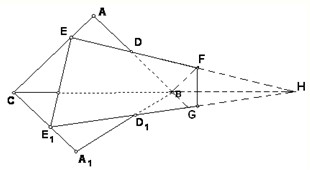
解：（1）互相平行或三线共点．
当BC∥平面DEE1D1时，平面ABC∩平面DEE1D1=ED
∴BC∥ED，
同理CB∥E1 D1，∴ED∥CB∥E1 D1
当BC不平行平面DEE1D1时，延长ED、CB交于点H，
∴H∈EF
∵EF?平面DEE1D1，∴H∈平面DEE1D1
同理H∈平面A1BC
∴H∈平面DEE1D1∩平面A1BC
即H∈E1D1
∴E1、D1、H三点共线，∴三线共点
（2）∵BC∥平面DEE1D1，且BC?平面ABC，平面ABC∩平面DEE1D1=ED
∴BC∥ED，同理BC∥E1D1
在△ABC中，BC∥ED，∴
=
同理可得
=
∴
•
•
•
=
•
•
•
=1
（3）由（1）可得，延长ED、CB、E1D1交于点H，过点B作BF∥AC，BG∥A1C
∵BF∥AC，∴
=
同理可得
=
在△HCE中，BG∥CE1，∴
=
同理可得
=
∴
•
•
•
=
•
•
•
=
×
=
×
=1
∴
•
•
•
的值不变化，仍为1
解：（1）互相平行或三线共点．当BC∥平面DEE1D1时，平面ABC∩平面DEE1D1=ED
∴BC∥ED，
同理CB∥E1 D1，∴ED∥CB∥E1 D1
当BC不平行平面DEE1D1时，延长ED、CB交于点H，
∴H∈EF
∵EF?平面DEE1D1，∴H∈平面DEE1D1
同理H∈平面A1BC
∴H∈平面DEE1D1∩平面A1BC
即H∈E1D1
∴E1、D1、H三点共线，∴三线共点
（2）∵BC∥平面DEE1D1，且BC?平面ABC，平面ABC∩平面DEE1D1=ED
∴BC∥ED，同理BC∥E1D1
在△ABC中，BC∥ED，∴
| AD |
| DB |
| AE |
| EC |
同理可得
| BD1 |
| D1A1 |
| CE1 |
| E1A1 |
∴
| AD |
| DB |
| BD1 |
| D1A1 |
| A1E1 |
| E1C |
| CE |
| EA |
| AE |
| EC |
| CE1 |
| E1A1 |
| A1E1 |
| E1C |
| CE |
| EA |
（3）由（1）可得，延长ED、CB、E1D1交于点H，过点B作BF∥AC，BG∥A1C
∵BF∥AC，∴
| AD |
| DB |
| AE |
| BF |
同理可得
| BD1 |
| D1A1 |
| BG |
| E1A1 |
在△HCE中，BG∥CE1，∴
| BG |
| CE1 |
| HB |
| HC |
同理可得
| FB |
| EC |
| HB |
| HC |
∴
| AD |
| DB |
| BD1 |
| D1A1 |
| A1E1 |
| E1C |
| CE |
| EA |
| AE |
| BF |
| BG |
| E1A1 |
| A1E1 |
| E1C |
| CE |
| EA |
| BG |
| CE1 |
| EC |
| FB |
| HB |
| HC |
| HC |
| HB |
∴
| AD |
| DB |
| BD1 |
| D1A1 |
| A1E1 |
| E1C |
| CE |
| EA |
点评：本题考查线面平行，考查平行线的性质，考查学生的计算能力，属于中档题．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
）第一题满分5分，第二题满分5分，第三题满分8分．
条交线ED,CB, E1 D1的关系。
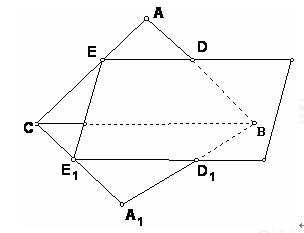
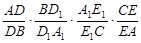的值;
的值;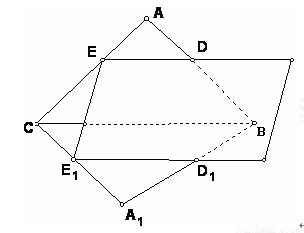
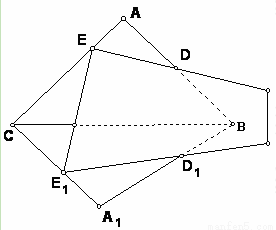
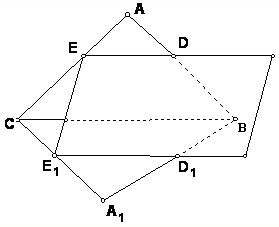如图，有一公共边但不共面的两个三角形ABC和A1BC被一平面DEE1D1所截，若平面DEE1D1分别交AB，AC，A1B，A1C于点D，E，D1，E1．
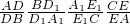的值；