题目内容
已知a,b∈R+,直线bx-ay-ab=0始终平分圆(x-1)2+(y+4)2=4,则a+b的最小值为________.
9
分析:由题意可知直线经过圆的圆心,求出圆的圆心,代入直线方程得到a,b的关系,然后利用基本不等式求出a+b的最小值.
解答:圆(x-1)2+(y+4)2=4圆心为(1,-4),
因为直线bx-ay-ab=0(a>0,b>0)始终平分圆(x-1)2+(y+4)2=4,所以直线经过圆的圆心,
所以4a+b-ab=0,
即 =1,(a>0,b>0)
=1,(a>0,b>0)
∴a+b=(a+b)( )=5+
)=5+ ≥5+2
≥5+2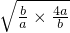 =9
=9
当且仅当 ,即a=3,b=6时,a+b的最小值为9
,即a=3,b=6时,a+b的最小值为9
故答案为:9
点评:本题考查直线与圆的位置关系,基本不等式的应用,注意等号成立的条件,考查计算能力,属于中档题.
分析:由题意可知直线经过圆的圆心,求出圆的圆心,代入直线方程得到a,b的关系,然后利用基本不等式求出a+b的最小值.
解答:圆(x-1)2+(y+4)2=4圆心为(1,-4),
因为直线bx-ay-ab=0(a>0,b>0)始终平分圆(x-1)2+(y+4)2=4,所以直线经过圆的圆心,
所以4a+b-ab=0,
即
 =1,(a>0,b>0)
=1,(a>0,b>0)∴a+b=(a+b)(
 )=5+
)=5+ ≥5+2
≥5+2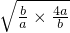 =9
=9当且仅当
 ,即a=3,b=6时,a+b的最小值为9
,即a=3,b=6时,a+b的最小值为9故答案为:9
点评:本题考查直线与圆的位置关系,基本不等式的应用,注意等号成立的条件,考查计算能力,属于中档题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
下列说法正确的是( )
| A、命题:“已知函数f(x),若f(x+1)与f(x-1)均为奇函数,则f(x)为奇函数,”为直命题 | B、“x>1”是“|x|>1”的必要不充分条件 | C、若“p且q”为假命题,则p,q均为假命题 | D、命题p:”?x∈R,使得x2+x+1<0”,则?p:”?x∈R,均有x2+x+1≥0” |
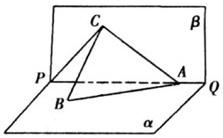 如图所示,PQ为平面α、β的交线,已知二面角α-PQ-β为直二面角,A∈PQ,B∈α,C∈β,CA=CB=kAB(k∈R*),∠BAP=45°.
如图所示,PQ为平面α、β的交线,已知二面角α-PQ-β为直二面角,A∈PQ,B∈α,C∈β,CA=CB=kAB(k∈R*),∠BAP=45°.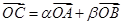 ,其中
,其中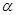
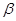 ∈R且
∈R且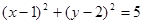 B.3x+2y-11=0 C.2x-y=0 D.x+2y=5
B.3x+2y-11=0 C.2x-y=0 D.x+2y=5