题目内容
设地球半径为R，在北纬30°圈上有甲、乙两地，它们的经度差为120°，那么这两地间的纬线之长为（ ）A．
πRB．
πRC．πR
D．2πR
【答案】分析：设北纬30°圈所在的小圆圆心为Q，地球球心为O，甲、乙两地分别对应A、B两点，作出如图辅助线，在Rt△OAQ中，可得AQ=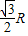
，再在圆Q中，根据A、B的经度差为120°，利用弧长公式即可得到弧AB的长．
解答：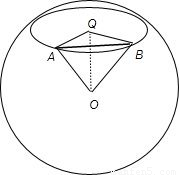
解：如图所示，设球心为O，北纬30°圈所在的小圆圆心为Q，甲、乙两地分别对应A、B两点
连接QO、QA、QB、OA、OB，
则OQ⊥平面QAB，∠OAQ=30°，∠AQB=120°=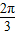
，
在Rt△OAQ中，OA=R，可得AQ=OAcos∠OAQ=Rcos30°=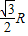
在圆Q中，A、B的经度差为120°，
∴弧AB的长为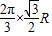
=
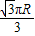
即两地间的纬线之长为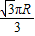
故选B．
点评：地球上的纬度是线面角，经度是面面角，求两地间的纬线之长，要用弧长公式，属于基础题．
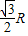，再在圆Q中，根据A、B的经度差为120°，利用弧长公式即可得到弧AB的长．解答：
解：如图所示，设球心为O，北纬30°圈所在的小圆圆心为Q，甲、乙两地分别对应A、B两点连接QO、QA、QB、OA、OB，
则OQ⊥平面QAB，∠OAQ=30°，∠AQB=120°=
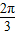，在Rt△OAQ中，OA=R，可得AQ=OAcos∠OAQ=Rcos30°=
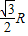
在圆Q中，A、B的经度差为120°，
∴弧AB的长为
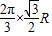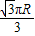
=即两地间的纬线之长为
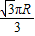
故选B．
点评：地球上的纬度是线面角，经度是面面角，求两地间的纬线之长，要用弧长公式，属于基础题．
练习册系列答案
巧学巧练系列答案
相关题目
设地球半径为R，如果A、B两点在北伟30°的纬线上，它们的经度差为60°，则A、B两点的球面距离为（ ）
A、R•arccos
| ||
B、R•arccos
| ||
C、
| ||
D、
|
，则A、B两点的球面距离为 （ ）
B．
C．
D．
，则A、B两点的球面距离为 （ ）
B．
C．
D．
，则A、B两点的球面距离为 （ ）
B．
C．
D．
，则A、B两点的球面距离为 （ ）
B．
C．
D．