题目内容
设命题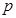 :“方程
:“方程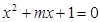 有两个实数根”;命题
有两个实数根”;命题 :“方程
:“方程 无实根”,若
无实根”,若 为假,
为假, 为假,求实数
为假,求实数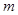 的取值范围.
的取值范围.
【答案】
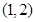 .
.
【解析】本试题考查了命题的真值问题的运用。因为若方程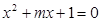 有两个实根,则
有两个实根,则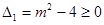 ,并且若方程
,并且若方程 无实根,则
无实根,则 ,根据已知
,根据已知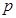 假
假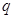 真,这样可以解答得到结论。
真,这样可以解答得到结论。
解:若方程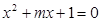 有两个实根,则
有两个实根,则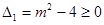 ,
,
解得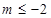 或
或
 ,
即
,
即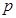 :
: 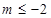 或
或
 ; …………………………4分
; …………………………4分
若方程 无实根,则
无实根,则 ,
,
解得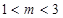 , 即
, 即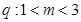 .
………………………………………8分
.
………………………………………8分
由于若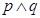 为假,则
为假,则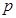 ,
,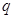 至少有一个为假;又
至少有一个为假;又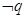 为假,则
为假,则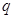 真.所以
真.所以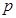 为假,
为假,
即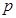 假
假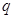 真,从而有
真,从而有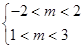 解得
解得 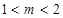 . ……………………11分
. ……………………11分
所以,实数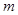 的取值范围是
的取值范围是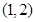 . ……………………………………………12分
. ……………………………………………12分

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
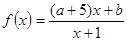 在(0,+
在(0,+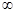 )上是增函数;命题q:方程
)上是增函数;命题q:方程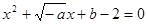 有两个不相等的负实数根,若p
有两个不相等的负实数根,若p q是真命题。
q是真命题。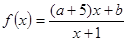 在
在 上是增函数;命题q:方程
上是增函数;命题q:方程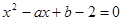 有两个不相等的负实数根。求使得p
有两个不相等的负实数根。求使得p q是真命题的实数对
q是真命题的实数对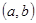 为坐标的点的轨迹图形及其面积。
为坐标的点的轨迹图形及其面积。 :“方程
:“方程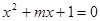 有两个实数根”;命题
有两个实数根”;命题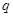 :“方程
:“方程 无实根”,若
无实根”,若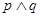 为假,
为假,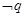 为假,求实数
为假,求实数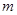 的取值范围.
的取值范围. “关于的x方程
“关于的x方程 有两个实数根”,命题
有两个实数根”,命题 “关于x的不等式
“关于x的不等式 对
对 恒成立”,若
恒成立”,若 为假,
为假, 为假,求实数
为假,求实数 的取值范围.
的取值范围.