题目内容
设不等式组
|
(Ⅰ)求曲线C的方程;
(Ⅱ)过点F(2,0)的直线与曲线C交于A,B两点.若以线段AB为直径的圆与y轴相切,求线段AB的长.
分析:(Ⅰ)动点P(x,y),根据题意可知
×
=1,整理得|x2-y2|=2.根据P∈D推断出x+y>0,x-y>0,进而可得x2-y2>0,答案可得.
(Ⅱ)设A(x1,y1),B(x2,y2),进而可得以线段AB为直径的圆的圆心Q的坐标,根据以线段AB为直径的圆与y轴相切,推断r=
|AB|=
.进而根据双曲线定义得|AB|=|AF|+|BF|,进而求得x1+x2的值,求得线段AB的长.
| |x+y| | ||
|
| |x-y| | ||
|
(Ⅱ)设A(x1,y1),B(x2,y2),进而可得以线段AB为直径的圆的圆心Q的坐标,根据以线段AB为直径的圆与y轴相切,推断r=
| 1 |
| 2 |
| x1+x2 |
| 2 |
解答: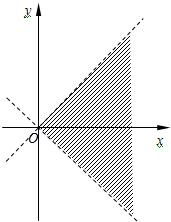 解:(Ⅰ)由题意可知,平面区域D如图阴影所示.
解:(Ⅰ)由题意可知,平面区域D如图阴影所示.
设动点P(x,y),则
×
=1,
即|x2-y2|=2.
∵P∈D、
∴x+y>0,x-y>0,即x2-y2>0.
∴x2-y2=2(x>0).
即曲线C的方程为
-
=1(x>0).
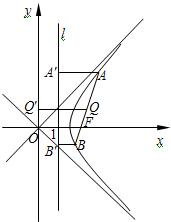
(Ⅱ)设A(x1,y1),B(x2,y2),
∴以线段AB为直径的圆的圆心Q(
,
),
∵以线段AB为直径的圆与y轴相切,
∴半径r=
|AB|=
.
即|AB|=x1+x2.①
∵曲线C的方程为
-
=1(x>0),
∴F(2,0)为其焦点,相应的准线方程为x=1,离心率e=
.
根据双曲线的定义可得,
=
=
,
∴|AB|=|AF|+|BF|=
(x1-1)+
(x2-1)=
(x1+x2)-2
.②
由①,②可得,x1+x2=
(x1+x2)-2
.
由此可得x1+x2=4+2
.
∴线段AB的长为4+2
.
 解:(Ⅰ)由题意可知,平面区域D如图阴影所示.
解:(Ⅰ)由题意可知,平面区域D如图阴影所示.设动点P(x,y),则
| |x+y| | ||
|
| |x-y| | ||
|
即|x2-y2|=2.
∵P∈D、
∴x+y>0,x-y>0,即x2-y2>0.
∴x2-y2=2(x>0).
即曲线C的方程为
| x2 |
| 2 |
| y2 |
| 2 |
(Ⅱ)设A(x1,y1),B(x2,y2),
∴以线段AB为直径的圆的圆心Q(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
∵以线段AB为直径的圆与y轴相切,
∴半径r=
| 1 |
| 2 |
| x1+x2 |
| 2 |

即|AB|=x1+x2.①
∵曲线C的方程为
| x2 |
| 2 |
| y2 |
| 2 |
∴F(2,0)为其焦点,相应的准线方程为x=1,离心率e=
| 2 |
根据双曲线的定义可得,
| |AF| |
| x1-1 |
| |BF| |
| x2-1 |
| 2 |
∴|AB|=|AF|+|BF|=
| 2 |
| 2 |
| 2 |
| 2 |
由①,②可得,x1+x2=
| 2 |
| 2 |
由此可得x1+x2=4+2
| 2 |
∴线段AB的长为4+2
| 2 |
点评:本题主要考查了双曲线的标准方程和直线与双曲线的关系.考查了学生综合分析问题和运算能力.

练习册系列答案
相关题目
设不等式组
表示的平面区域为D,若指数函数y=ax的图象上存在区域D上的点,则a的取值范围是( )
|
| A、(1,3] |
| B、[2,3] |
| C、(1,2] |
| D、[3,+∞] |