题目内容
已知函数 ,
, ,其中无理数e=2.17828….
,其中无理数e=2.17828….(Ⅰ)若P=0,求证:f(x)>1-x;
(Ⅱ)若在其定义域内f(x)是单调函数,求P的取值范围;
(Ⅲ)对于区间(1,2)中的任意常数P,是否存在x>0,使f(x)≤g(x)成立?若存在,求出符合条件的一个x;否则说明理由.
【答案】分析:(Ⅰ)若P=0,要证f(x)>1-x;即可转化为lnx-x+1>0在定义域内恒成立即可.在通过求导,研究其单调性,看函数的最小值,只要函数的最小值大于0即可.
(Ⅱ)若在其定义域内f(x)是单调函数,求P的取值范围;先要明确定义域;在求导,求导后,只要满足导数在某区间恒大于0或在某区间恒小于0即可.在这里要注意对参数p进行讨论.
(Ⅲ)对于区间(1,2)中的任意常数P,是否存在x>0,使f(x)≤g(x)成立,这种题型属探索性问题;解决的关键在于弄懂题意.据题意可转化为:令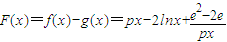 ,则问题等价于找一个x>0使F(x)≤0成立,
,则问题等价于找一个x>0使F(x)≤0成立,
故只需满足函数的最小值F(x)min≤0即可.
解答:解:(Ⅰ)证明:当p=0时,f(x)=-lnx.
令m(x)=lnx-x+1,则 .
.
若0<x<1,m′(x)>0,m(x)递增;
若x>1,m′(x)<0,m(x)递减,
则x=1是m(x)的极(最)大值点.
于是m(x)≤m(1)=0,即lnx-x+1≤0.
故当p=0时,有f(x)≥1-x;(4分)
(Ⅱ)解:对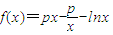 求导,
求导,
得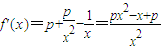 .
.
①若p=0,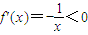 ,
,
则f(x)在(0,+∞)上单调递减,故p=0合题意.
②若p>0,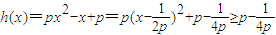 .
.
则必须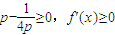 ,
,
故当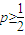 时,f(x)在(0,+∞)上单调递增.
时,f(x)在(0,+∞)上单调递增.
③若p<0,h(x)的对称轴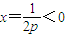 ,
,
则必须h(0)≤0,f′(x)≤0,
故当p<0时,f(x)在(0,+∞)上单调递减.
综合上述,p的取值范围是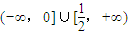 ;
;
(Ⅲ)解:令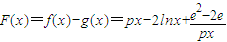 .
.
则问题等价于找一个x>0使F(x)≤0成立,
故只需满足函数的最小值F(x)min≤0即可.
因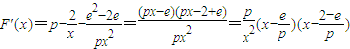 ,
,
而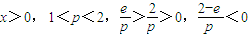 ,
,
故当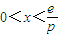 时,F′(x)<0,F(x)递减;
时,F′(x)<0,F(x)递减;
当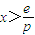 时,F′(x)>0,F(x)递增.
时,F′(x)>0,F(x)递增.
于是,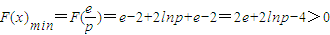 .
.
与上述要求F(x)min≤0相矛盾,故不存在符合条件的x.
点评:(1)若在其定义域内f(x)是单调函数,求参数的取值范围;先要明确定义域;在求导,求导后,只要满足导数在某区间恒大于0或在某区间恒小于0即可.这是通性通法.
(2)对于区间任意给定的某区间,某代数式恒成立问题,解决的关键在于弄懂题意.据题意一般可可转化为构造一个函数,求满足函数的最小值或者函数的最大值即可.
(Ⅱ)若在其定义域内f(x)是单调函数,求P的取值范围;先要明确定义域;在求导,求导后,只要满足导数在某区间恒大于0或在某区间恒小于0即可.在这里要注意对参数p进行讨论.
(Ⅲ)对于区间(1,2)中的任意常数P,是否存在x>0,使f(x)≤g(x)成立,这种题型属探索性问题;解决的关键在于弄懂题意.据题意可转化为:令
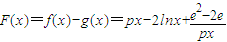 ,则问题等价于找一个x>0使F(x)≤0成立,
,则问题等价于找一个x>0使F(x)≤0成立,故只需满足函数的最小值F(x)min≤0即可.
解答:解:(Ⅰ)证明:当p=0时,f(x)=-lnx.
令m(x)=lnx-x+1,则
 .
.若0<x<1,m′(x)>0,m(x)递增;
若x>1,m′(x)<0,m(x)递减,
则x=1是m(x)的极(最)大值点.
于是m(x)≤m(1)=0,即lnx-x+1≤0.
故当p=0时,有f(x)≥1-x;(4分)
(Ⅱ)解:对
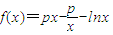 求导,
求导,得
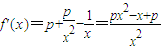 .
.①若p=0,
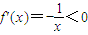 ,
,则f(x)在(0,+∞)上单调递减,故p=0合题意.
②若p>0,
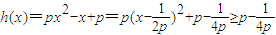 .
.则必须
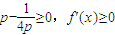 ,
,故当
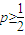 时,f(x)在(0,+∞)上单调递增.
时,f(x)在(0,+∞)上单调递增.③若p<0,h(x)的对称轴
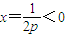 ,
,则必须h(0)≤0,f′(x)≤0,
故当p<0时,f(x)在(0,+∞)上单调递减.
综合上述,p的取值范围是
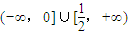 ;
;(Ⅲ)解:令
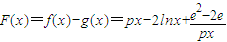 .
.则问题等价于找一个x>0使F(x)≤0成立,
故只需满足函数的最小值F(x)min≤0即可.
因
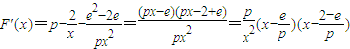 ,
,而
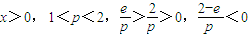 ,
,故当
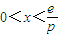 时,F′(x)<0,F(x)递减;
时,F′(x)<0,F(x)递减;当
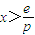 时,F′(x)>0,F(x)递增.
时,F′(x)>0,F(x)递增.于是,
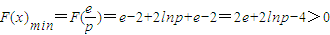 .
.与上述要求F(x)min≤0相矛盾,故不存在符合条件的x.
点评:(1)若在其定义域内f(x)是单调函数,求参数的取值范围;先要明确定义域;在求导,求导后,只要满足导数在某区间恒大于0或在某区间恒小于0即可.这是通性通法.
(2)对于区间任意给定的某区间,某代数式恒成立问题,解决的关键在于弄懂题意.据题意一般可可转化为构造一个函数,求满足函数的最小值或者函数的最大值即可.

练习册系列答案
相关题目
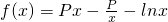 ,
,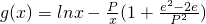 ,其中无理数e=2.17828….
,其中无理数e=2.17828….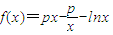 ,
,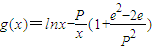 ,其中无理数e=2.17828….
,其中无理数e=2.17828…. ,
, ,其中无理数e=2.17828….
,其中无理数e=2.17828….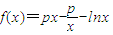 ,
, ,其中无理数e=2.17828….
,其中无理数e=2.17828….