题目内容
给出下面四个命题:① 函数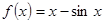 (
(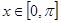 )的最大值为
)的最大值为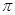 ,最小值为
,最小值为 ;② 函数y=x3-12x (-3<x<2)的最大值为16,最小值为-16;③ 函数y=x3-12x (-2<x<2)无最大值,也无最小值;④函数
;② 函数y=x3-12x (-3<x<2)的最大值为16,最小值为-16;③ 函数y=x3-12x (-2<x<2)无最大值,也无最小值;④函数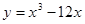 在
在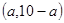 上有最小值,则
上有最小值,则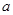 的取值范围是
的取值范围是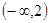 。 其中正确的命题有( )
。 其中正确的命题有( )
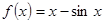 (
(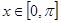 )的最大值为
)的最大值为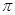 ,最小值为
,最小值为 ;② 函数y=x3-12x (-3<x<2)的最大值为16,最小值为-16;③ 函数y=x3-12x (-2<x<2)无最大值,也无最小值;④函数
;② 函数y=x3-12x (-3<x<2)的最大值为16,最小值为-16;③ 函数y=x3-12x (-2<x<2)无最大值,也无最小值;④函数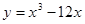 在
在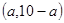 上有最小值,则
上有最小值,则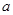 的取值范围是
的取值范围是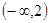 。 其中正确的命题有( )
。 其中正确的命题有( ) | A.1个 | B.2个 | C.3个 | D.4个 |
B
解:
①函数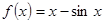 (
(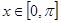 )的最大值为
)的最大值为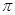 ,最小值为
,最小值为 ;利用求导,判定递增得到结论成立。
;利用求导,判定递增得到结论成立。
② 函数y=x3-12x (-3<x<2)的最大值为16,最小值为-16;求导数得到无最小值,错误。
③ 函数y=x3-12x (-2<x<2)无最大值,也无最小值;成立。
④函数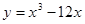 在
在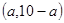 上有最小值,则
上有最小值,则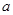 的取值范围是
的取值范围是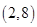 因此错误。
因此错误。
①函数
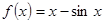 (
(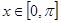 )的最大值为
)的最大值为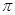 ,最小值为
,最小值为 ;利用求导,判定递增得到结论成立。
;利用求导,判定递增得到结论成立。② 函数y=x3-12x (-3<x<2)的最大值为16,最小值为-16;求导数得到无最小值,错误。
③ 函数y=x3-12x (-2<x<2)无最大值,也无最小值;成立。
④函数
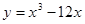 在
在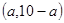 上有最小值,则
上有最小值,则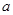 的取值范围是
的取值范围是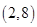 因此错误。
因此错误。
练习册系列答案
相关题目

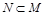

 .设集合
.设集合 ,
,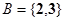 ,则集合
,则集合 的所有元素之和为 ( )
的所有元素之和为 ( ) R
R
 M
M N*
N*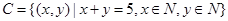 _______.
_______.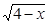 +lg(3
+lg(3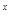 -9)的定义域为A,集合B=
-9)的定义域为A,集合B=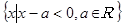 ,
,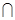 B。
B。 的实数全体
的实数全体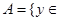 Z
Z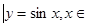 R
R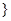 ,则集合
,则集合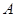 的子集的个数为( )
的子集的个数为( )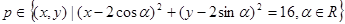 ,则满足条件的点在平面上组成的图形的面积为_______
,则满足条件的点在平面上组成的图形的面积为_______


