题目内容
给出下列四个命题,其中不正确命题的序号是 。
①若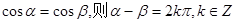 ;②函数
;②函数 的图象关于x=
的图象关于x= 对称;③函数
对称;③函数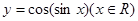 为偶函数,④函数
为偶函数,④函数 是周期函数,且周期为2
是周期函数,且周期为2 。
。
①②④
解析试题分析:由诱导公式,我们根据cosα=cosβ可判断①的真假;根据余弦函数的对称性,可判断②的真假;根据函数奇偶性的定义,可判断③的真假;根据函数周期性可以判断④的真假,进而得到答案.解:若cosα=cosβ,则α-β=2kπ,或α+β=2kπ,k∈Z,故①不正确;函数y=2cos(2x+ )的图象关于(
)的图象关于( ,0)中心对称,故②不正确;由函数f(-x)=cos[sin(-x)]=cos(sinx)(x∈R),故f(x)为偶函数,故③正确;函数y=sin|x|是周期函数,且周期为π,故④不正确.故答案为:①②④
,0)中心对称,故②不正确;由函数f(-x)=cos[sin(-x)]=cos(sinx)(x∈R),故f(x)为偶函数,故③正确;函数y=sin|x|是周期函数,且周期为π,故④不正确.故答案为:①②④
考点:命题的真假判断,三角函数的周期性
点评:本题考查的知识点是命题的真假判断与应用,三角函数的周期性及其求法,余弦函数的奇偶性,余弦函数的对称性,熟练掌握三角函数的性质是解答本题的关键

练习册系列答案
相关题目
 ”是“
”是“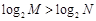 ”成立的 条件.(从“充要”,“充分不必要”,“必要不充分”中选择一个正确的填写)
”成立的 条件.(从“充要”,“充分不必要”,“必要不充分”中选择一个正确的填写) :
: ,
, :
: ,若
,若 的充分不必要条件,则实数
的充分不必要条件,则实数 的取值范围是 .
的取值范围是 .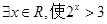 ”的否定是“
”的否定是“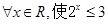 ”;
”; 的最小正周期是
的最小正周期是
 处有极值,则
处有极值,则 ”的否命题是真命题;
”的否命题是真命题; 上的奇函数,
上的奇函数, 时的解析式是
时的解析式是 ,则
,则 时的解析式为
时的解析式为 其中正确的说法是 。
其中正确的说法是 。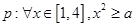 ,命题
,命题 若命“
若命“ ”是真命题,则实数
”是真命题,则实数 的取值范围为 .
的取值范围为 .  (其中
(其中 为整数),则
为整数),则 最近的整数,记作
最近的整数,记作 ,即
,即 . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数 的四个命题:
的四个命题: 的定义域是
的定义域是 ,值域是
,值域是 ;
; 是
是 ;
; ;
; 上是增函数.
上是增函数.  :
: , 则
, 则
 ,则
,则 ”的逆否命题为_________
”的逆否命题为_________