题目内容
为了了解大学生在购买饮料时看营养说明是否与性别有关,对某班50人进行问卷调查得到2×2列联表.| 看说明 | 不看说明 | 合计 | |
| 女生 | 5 | ||
| 男生 | 10 | ||
| 合计 | 50 |
| 3 |
| 5 |
(Ⅰ)请将上面2×2列联表补充完整;
(Ⅱ)已知看营养说明的10位男生中,同时看生产日期的有A1、A2、A3、A4、A5;同时看生产厂家的有Bl、B2、B3:同时看保质期的有C1、C2.现从看生产日期、看生产厂家、看保质期的男生中各选出一名进行其他方面的调查,求B1和C1不全被选中的概率;
(Ⅲ)是否有99.5%的把握认为“看营养说明与性别有关”?说明你的理由.
分析:(I)根据全部50人中随机抽取1人看营养说明的学生的概率为
,做出看营养说明的人数,这样用总人数减去看营养说明的人数,剩下的是不看的,根据所给的另外两个数字,填上所有数字.
(II)B1和C1不全被选中D的对立事件是两个全被选中,两个都被选中是一个等可能事件的概率,做出试验发生包含的事件数和满足条件的事件数,做出概率,用1减去求得的概率得到要求的结果.
(III)根据列联表所给的数据,代入求观测值的公式,把观测值同临界值进行比较,得到有99.5%的把握说看营养说明与性别有关.
| 3 |
| 5 |
(II)B1和C1不全被选中D的对立事件是两个全被选中,两个都被选中是一个等可能事件的概率,做出试验发生包含的事件数和满足条件的事件数,做出概率,用1减去求得的概率得到要求的结果.
(III)根据列联表所给的数据,代入求观测值的公式,把观测值同临界值进行比较,得到有99.5%的把握说看营养说明与性别有关.
解答:解:(I)∵全部50人中随机抽取1人看营养说明的学生的概率为
.
∴看营养说明的有
×50=30,
∴不看营养说明的有50-20=30
∴列联表是
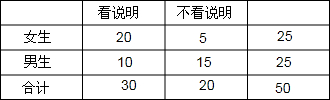
(II)B1和C1不全被选中D的对立事件是两个全被选中,
∵两个都被选中是一个等可能事件的概率,
试验发生包含的事件是5×3×2=30,
满足条件的事件数C51=5,
∴根据等可能事件的概率得到P=
=
,
∴B1和C1不全被选中的概率P=1-
=
(III)由列联表可得K2=
=8.333>7.879
∴有99.5%的把握说看营养说明与性别有关.
| 3 |
| 5 |
∴看营养说明的有
| 3 |
| 5 |
∴不看营养说明的有50-20=30
∴列联表是

(II)B1和C1不全被选中D的对立事件是两个全被选中,
∵两个都被选中是一个等可能事件的概率,
试验发生包含的事件是5×3×2=30,
满足条件的事件数C51=5,
∴根据等可能事件的概率得到P=
| 5 |
| 30 |
| 1 |
| 6 |
∴B1和C1不全被选中的概率P=1-
| 1 |
| 6 |
| 5 |
| 6 |
(III)由列联表可得K2=
| 50×(20×15-10×5)2 |
| 30×20×25×25 |
∴有99.5%的把握说看营养说明与性别有关.
点评:本题考查画出列联表,考查等可能事件的概率,考查独立性检验,在求观测值时,要注意数字的代入和运算不要出错.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
为了了解大学生在购买饮料时看营养说明是否与性别有关,对某班50人进行问卷调查得到2×2列联表.
已知在全部50人中随机抽取1人看营养说明的学生的概率为
.
(Ⅰ)请将上面2×2列联表补充完整;
(Ⅱ)是否有99.5%的把握认为“看营养说明与性别有关”?说明你的理由.
(Ⅲ)从看营养说明的10位男生中抽出7名进行调查,其中看生产日期的有A1、A2、A3,看生产厂家的有B1、B2,看保质期的有C1、C2,现从看生产日期、看生产厂家、看保质期的男生中各选出1名进行其他方面的调查,求B1和C1不全被选中的概率.
| 看说明 | 不看说明 | 合计 | |
| 女生 | 5 | ||
| 男生 | 10 | ||
| 合计 | 50 |
| 3 |
| 5 |
(Ⅰ)请将上面2×2列联表补充完整;
(Ⅱ)是否有99.5%的把握认为“看营养说明与性别有关”?说明你的理由.
(Ⅲ)从看营养说明的10位男生中抽出7名进行调查,其中看生产日期的有A1、A2、A3,看生产厂家的有B1、B2,看保质期的有C1、C2,现从看生产日期、看生产厂家、看保质期的男生中各选出1名进行其他方面的调查,求B1和C1不全被选中的概率.
为了了解大学生在购买饮料时看营养说明是否与性别有关,对某班50人进行问卷调查得到2×2列联表.
| 看说明 | 不看说明 | 合计 | |
| 女生 | 5 | ||
| 男生 | 10 | ||
| 合计 | 50 |
 .
.(Ⅰ)请将上面2×2列联表补充完整;
(Ⅱ)已知看营养说明的10位男生中,同时看生产日期的有A1、A2、A3、A4、A5;同时看生产厂家的有Bl、B2、B3:同时看保质期的有C1、C2.现从看生产日期、看生产厂家、看保质期的男生中各选出一名进行其他方面的调查,求B1和C1不全被选中的概率;
(Ⅲ)是否有99.5%的把握认为“看营养说明与性别有关”?说明你的理由.
为了了解大学生在购买饮料时看营养说明是否与性别有关,对某班50人进行问卷调查得到2×2列联表.
已知在全部50人中随机抽取1人看营养说明的学生的概率为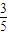 .
.
(Ⅰ)请将上面2×2列联表补充完整;
(Ⅱ)已知看营养说明的10位男生中,同时看生产日期的有A1、A2、A3、A4、A5;同时看生产厂家的有Bl、B2、B3:同时看保质期的有C1、C2.现从看生产日期、看生产厂家、看保质期的男生中各选出一名进行其他方面的调查,求B1和C1不全被选中的概率;
(Ⅲ)是否有99.5%的把握认为“看营养说明与性别有关”?说明你的理由.
| 看说明 | 不看说明 | 合计 | |
| 女生 | 5 | ||
| 男生 | 10 | ||
| 合计 | 50 |
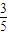 .
.(Ⅰ)请将上面2×2列联表补充完整;
(Ⅱ)已知看营养说明的10位男生中,同时看生产日期的有A1、A2、A3、A4、A5;同时看生产厂家的有Bl、B2、B3:同时看保质期的有C1、C2.现从看生产日期、看生产厂家、看保质期的男生中各选出一名进行其他方面的调查,求B1和C1不全被选中的概率;
(Ⅲ)是否有99.5%的把握认为“看营养说明与性别有关”?说明你的理由.
为了了解大学生在购买饮料时看营养说明是否与性别有关,对某班50人进行问卷调查得到2×2列联表.
已知在全部50人中随机抽取1人看营养说明的学生的概率为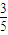 .
.
(Ⅰ)请将上面2×2列联表补充完整;
(Ⅱ)是否有99.5%的把握认为“看营养说明与性别有关”?说明你的理由.
(Ⅲ)从看营养说明的10位男生中抽出7名进行调查,其中看生产日期的有A1、A2、A3,看生产厂家的有B1、B2,看保质期的有C1、C2,现从看生产日期、看生产厂家、看保质期的男生中各选出1名进行其他方面的调查,求B1和C1不全被选中的概率.
| 看说明 | 不看说明 | 合计 | |
| 女生 | 5 | ||
| 男生 | 10 | ||
| 合计 | 50 |
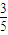 .
.(Ⅰ)请将上面2×2列联表补充完整;
(Ⅱ)是否有99.5%的把握认为“看营养说明与性别有关”?说明你的理由.
(Ⅲ)从看营养说明的10位男生中抽出7名进行调查,其中看生产日期的有A1、A2、A3,看生产厂家的有B1、B2,看保质期的有C1、C2,现从看生产日期、看生产厂家、看保质期的男生中各选出1名进行其他方面的调查,求B1和C1不全被选中的概率.