题目内容
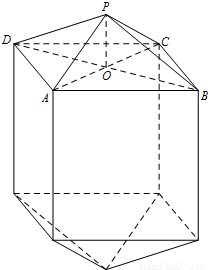
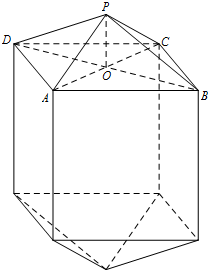 某公司拟制造如图所示的工件(长度单位:米),要求工件的体积为10立方米,其中工件的中间为长方体,上下两端为相同的正四棱锥,其底面边长AB=a,高PO=
某公司拟制造如图所示的工件(长度单位:米),要求工件的体积为10立方米,其中工件的中间为长方体,上下两端为相同的正四棱锥,其底面边长AB=a,高PO=| 3 | 8 |
(1)写出y关于a的函数表达式,并求该函数的定义域;
(2)求该工件的制造费用最小时a的值.
分析:(1)由长方体和四棱锥的体积的表达式,得到a和b的关系.再由柱和锥体的表面积公式建立关系式,将表达式中的b用a表示.并注意到写定义域时,利用b>0,求出自变量a的范围.
(2)用导数的知识解决,注意到定义域的限制,确定函数f(x)在定义域上的单调性,从而可求函数的最大值.
(2)用导数的知识解决,注意到定义域的限制,确定函数f(x)在定义域上的单调性,从而可求函数的最大值.
解答:解:(1)AB=a,PO=
a,∴斜高为
=
.…(2分)
∴一个正四棱锥的侧面积为S1=4×
×a×
=
a2.
一个正四棱锥的体积为V1=
a2×
a=
a3. …(4分)
令长方体的高为b,则a2b+
a3×2=10.∴b=
-
a. …(6分)
由b>0,得0<a<2
. …(8分)y=4ab×2+
a2×2×4=8ab+10a2=
+8a2,定义域为(0,2
).…(11分)
(2)y′=-
+16a,令y'=0,得a=
. …(13分)
当a∈(0,
),y'<0,y为a的减函数;
当a∈(
,2
),y'>0,y为a的增函数,…(15分)
(答)该工件的制造费用最小时,a的值为
(米). …(16分)
| 3 |
| 8 |
(
|
| 5a |
| 8 |
∴一个正四棱锥的侧面积为S1=4×
| 1 |
| 2 |
| 5a |
| 8 |
| 5 |
| 4 |
一个正四棱锥的体积为V1=
| 1 |
| 3 |
| 3 |
| 8 |
| 1 |
| 8 |
令长方体的高为b,则a2b+
| 1 |
| 8 |
| 10 |
| a2 |
| 1 |
| 4 |
由b>0,得0<a<2
| 3 | 5 |
| 5 |
| 4 |
| 80 |
| a |
| 3 | 5 |
(2)y′=-
| 80 |
| a2 |
| 3 | 5 |
当a∈(0,
| 3 | 5 |
当a∈(
| 3 | 5 |
| 3 | 5 |
(答)该工件的制造费用最小时,a的值为
| 3 | 5 |
点评:利用导数的知识研究函数单调性,函数最值问题是高考经常考查的知识点,同时考查空间想象力也蕴含在其中.

练习册系列答案
相关题目
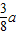 .假设工件的制造费用仅与其表面积有关,已知正四棱柱侧面每平方米制造费用为2千元,正四棱锥侧面每平方米建造费用为4千元.设工件的制造费用为y千元.
.假设工件的制造费用仅与其表面积有关,已知正四棱柱侧面每平方米制造费用为2千元,正四棱锥侧面每平方米建造费用为4千元.设工件的制造费用为y千元.