题目内容
“1＜k＜7”是“方程
+
=1表示双曲线”的（ ）
| x2 |
| k-2 |
| y2 |
| k-6 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、既不充分也不必要条件 |
| D、充要条件 |
分析：根据双曲线的标准方程对充分性与必要性分别加以论证，可得：当1＜k＜7成立时，方程不一定能表示双曲线；反之，若方程表示双曲线，建立关于k的不等式并解之得2＜k＜6，必定有1＜k＜7成立．由此可得本题答案．
解答：解：①先看充分性，
若1＜k＜7，则当k=
时，方程为
+
=1，不能表示双曲线，
因此充分性不能成立；
②再看必要性，若方程
+
=1表示双曲线，则（k-2）•（k-6）＜0，
解得2＜k＜6，必定有1＜k＜7成立，因此可得必要性成立．
综上所述，“1＜k＜7”是“方程
+
=1表示双曲线”的必要不充分条件．
故选：B．
若1＜k＜7，则当k=
| 3 |
| 2 |
| x2 | ||
-
|
| y2 | ||
-
|
因此充分性不能成立；
②再看必要性，若方程
| x2 |
| k-2 |
| y2 |
| k-6 |
解得2＜k＜6，必定有1＜k＜7成立，因此可得必要性成立．
综上所述，“1＜k＜7”是“方程
| x2 |
| k-2 |
| y2 |
| k-6 |
故选：B．
点评：本题给出含有参数k的二次曲线方程，判断方程表示双曲线的充要条件．着重考查了双曲线的标准方程与充要条件的判定等知识，属于中档题．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
相关题目
（2009•普宁市模拟）为了确保神州七号飞船发射时的信息安全，信息须加密传输，发送方由明文→密文（加密），接受方由密文→明文（解密），已知加密的方法是：密码把英文的明文（真实文）按字母分解，其中英文的a，b，c，…，z的26个字母（不论大小写）依次对应1，2，3，…，26这26个自然数（见下表）：
|
下列说法：
①将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变；
②设有一个回归方程
，变量x增加一个单位时，y平均增加5个单位；
③线性回归方程
必过（
）；
④在一个2×2列联中，由计算得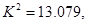
则有99%的把握确认这两个变量间有关系；
` 其中错误的个数是 （ ）
A．0 B．1 C．2 D．3
本题可以参考独立性检验临界值表：
|
|
0.5 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.25 |
0.010 |
0.005 |
0.001 |
|
k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.535 |
7.879 |
10.828 |
